Le macchine a flusso assiale, o macchine a disco, sono delle macchine sincrone a magneti permanenti con un ingombro assiale ridotto rispetto a quello radiale [1, 2, 3].

Nelle macchine tradizionali a flusso radiale il flusso al traferro è diretto in direzione radiale, mentre nelle macchine a flusso assiale il flusso è diretto assialmente. Le superfici utili per la produzione di coppia, cioè le superfici dove sono disposti i conduttori ed i magneti permanenti, sono perpendicolari all’asse.

La macchina a disco consente di ottenere valori di coppia specifica elevati perché le parti attive si trovano vicine alla circonferenza esterna e quindi lontano dall’asse di rotazione.

La possibilità di produrre il campo utilizzando dei magneti permanenti permette di  costruire una macchina sincrona con  numero di coppie di poli elevato, riuscendo a contenere il costo di produzione e l’ingombro. Inoltre, la macchina a disco non necessità di regolazione di tensione. Le velocità di rotazione sono basse rispetto a quelle dei motori elettrici convenzionali di piccola potenza (100÷500 rpm contro 1000 ÷3000 rpm).

La macchina a flusso assiale usata come motore offre ottime prestazioni nel campo della trazione elettrica e permette l’accoppiamento diretto con le ruote motrici. Sono stati costruiti motori con ingombro assiale così ridotto da poter essere inseriti nel mozzo delle ruote degli autoveicoli elettrici. L’assenza di giunti o riduttori meccanici interposti tra motore e ruota, con l’ulteriore possibilità di eliminare il differenziale meccanico nei veicoli a quattro ruote, costituiscono i vantaggi rilevanti nella scelta di questi motori.

La macchina a disco usata come generatore trova applicazioni soprattutto nei sistemi eolici con rendimenti elevati e assenza anche in questo caso di moltiplicatori di giri meccanici: l’accoppiamento avviene, infatti, calettando il generatore direttamente sull’asse della turbina.

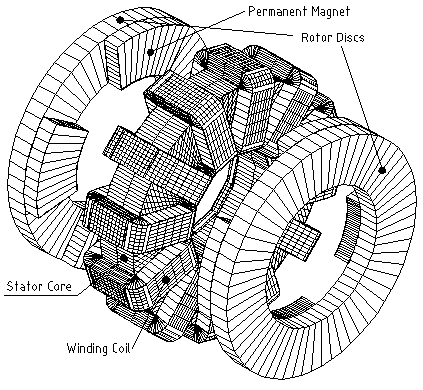
Sono possibili differenti configurazioni di macchina. In questa tesi si prenderà in considerazione una topologia simile a quella della Figura 1-1 in cui la macchina è composta da uno statore e due rotori:

– Lo statore è costituito da un nucleo a corona circolare realizzato avvolgendo a spirale una sottile striscia di materiale ferromagnetico.

Attorno al nucleo vengono avvolti i conduttori. Ciascuna bobina è sottoposta a due flussi ognuno dei quali è generato dai magneti di un rotore.

Nella tipologia descritta lo statore è privo di cave. Questa scelta permette di evitare ulteriori lavorazioni meccaniche con vantaggi pratici ed economici.

– I rotori sono disposti sui due lati esterni dello statore. I magneti dei due rotori si presentano con i poli magnetici uguali affacciati. Il flusso che entra nello statore lo attraversa quindi in direzione azimutale per poi uscire in direzione assiale sul passo polare adiacente. Il ferro di rotore non viene laminato perché è attraversato da un flusso magnetico praticamente costante nel tempo. Di conseguenza, nel rotore non ci sono perdite per isteresi e per correnti parassite.

Si può osservare come i magneti permanenti montati sui rotori presentano solo superfici piane, con conseguente facilità di costruzione e di montaggio degli stessi.

 I PARAMETRI CARATTERISTICI

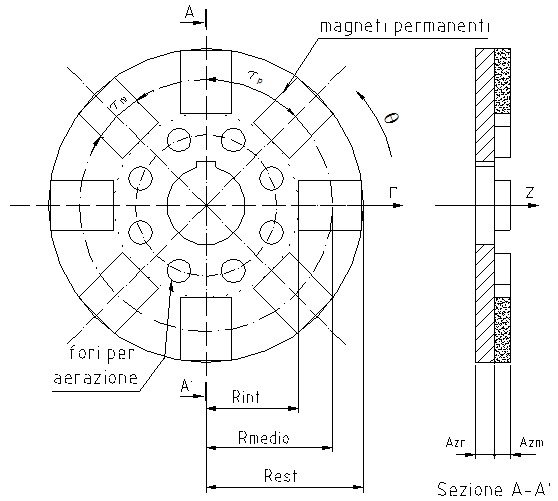
Nella Figura 1-2 è riportata la vista di un rotore di una macchina a flusso assiale. I simboli dello schema hanno il seguente significato:

 

Tabella 4  Simboli dimensionali della macchina a flusso assiale

Si nota che i magneti hanno una forma rettangolare ed il loro profilo non coincide con le circonferenze esterna ed interna della macchina. La scelta di una forma così semplice deriva da una maggiore facilità di costruzione del magnete: in quanto è più facile realizzare magneti di forma elementare. Proprio per questo motivo può risultare conveniente dare forma al polo di macchina con più di un magnete costruendo una tessellazione. Gli scopi di questa scelta potrebbero derivare da una maggiore facilità nel reperire taglie già presenti sul mercato o dalla necessità di ottenere forze elettromotrici indotte nelle bobine della macchina, più vicine a quelle desiderate.

Nella costruzione dell’algoritmo si assume come ipotesi semplificativa che il profilo del magnete segua le circonferenze esterna ed interna.

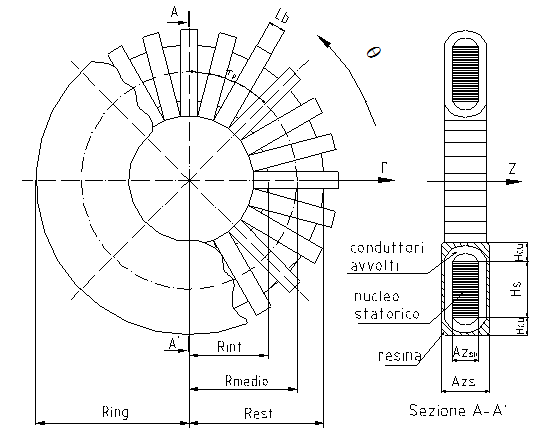
Le grandezze principali dello statore sono disegnate nella Figura 7:

In genere, la macchina a disco viene costruita in modo che lo spessore radiale di statore (Rest-Rint), sia uguale all’altezza dei magneti Hs (Hs = Rest-Rint ).

La Figura 8 riporta la sezione della macchina a disco con i due rotori agli estremi e statore al centro. Lo statore ha un ingombro radiale maggiore dei due rotori.

Nella Figura 8 sono introdotti dei nuovi simboli che hanno il seguente significato:

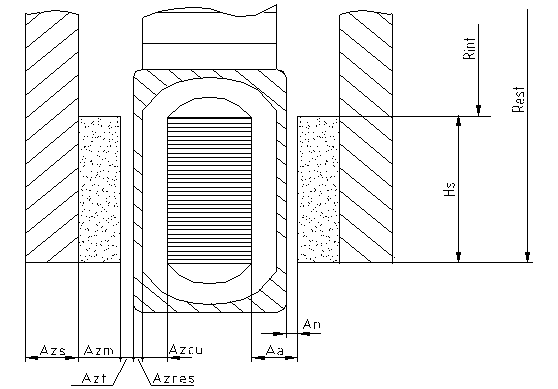
Tabella 5 Denominazione e nomenclatura della AFPM

Anche per la macchina a flusso assiale il numero di poli di un rotore deve essere pari. Un magnete orientato verso lo statore con un determinato polo magnetico deve avere a fianco due magneti con poli di segno opposto.

 Vista la definizione dei simboli  Nst, Ncp e p si calcola:

Numero di magneti:  

Numero di bobine: 

Numero di spire in una bobina:  

Numero totale di spire della macchina: 

Dopo aver definito tutti i simboli necessari per descrivere una macchina a disco si introducono delle semplici relazioni geometriche:

Raggio medio della macchina: 

Passo polare della macchina misurato sul raggio medio:  

Si introducono inoltre delle grandezze adimensionali. In seguito, si studierà l’influenza che questi coefficienti hanno sulle prestazioni della macchina.

Rapporto tra i raggi:

Fattore di forma del magnete:

                                                                                                  (1.2-8)

Frazione del passo polare occupata dal magnete (passo di magnete):

                                                                                                     (1.2-9)

Rapporto tra percorso del flusso di induzione in aria e nel magnete:

                                                                                                (1.2-10)

Coefficiente di sfruttamento superficiale del singolo conduttore (vedere Figura 1-5):

                                                                                           (1.2-11)

Figura 9  Conduttori smaltati a sezione circolare e a piattina

Quest’ultima relazione è valida per qualsiasi tipo di conduttore. Per conduttori di tipo circolare si può definire anche il coefficiente Kss’:

                                                                           (1.2-12)

Per le piattine si definisce il fattore di forma della sezione in rame Kc:

                                                                             (1.2-13)

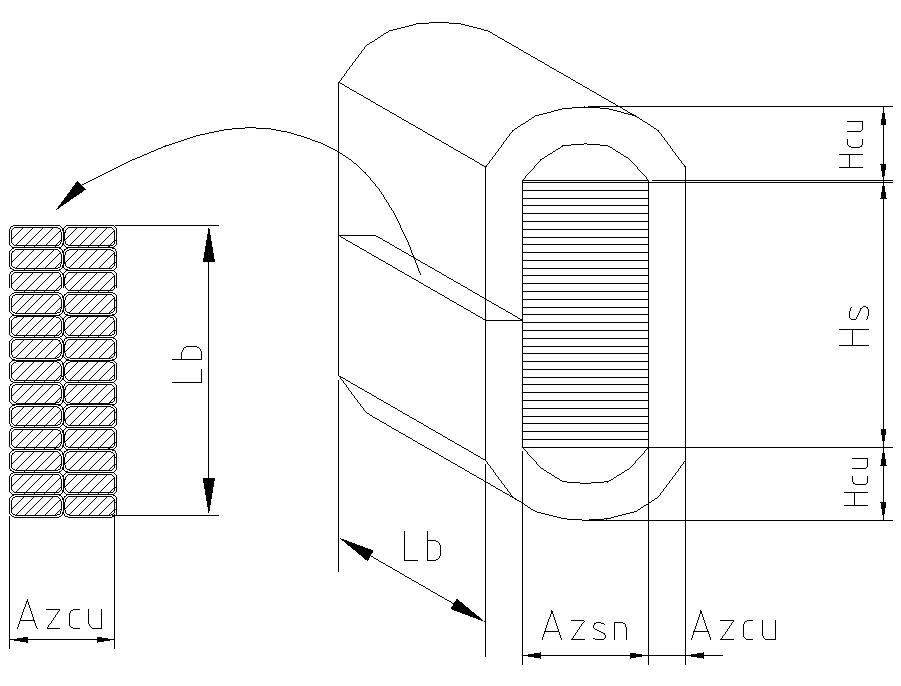
Il coefficiente di stipamento lineare per i conduttori di bobina è rappresentato dal parametro Kstl  ovvero Ksti. La grandezza Kstl  è misurata lungo la circonferenza interna alle testate (Figura 1-6) e vale:

                                                 (1.2-14)

  Questo coefficiente è sempre minore o uguale ad uno. Se Kstl=1 lo spazio disponibile  per lo stipamento viene tutto occupato dai conduttori avvolti.

  Studiando la funzione Kstl (1/R) con R tale che Rint• R • Rest si troverà una funzione decrescente con legge iperbolica. Questo vuol dire semplicemente che nella macchina a disco la superficie della corona non potrà mai essere interamente ricoperta dai conduttori.

 Sulla circonferenza di raggio interno Rint si misura invece il parametro  Ksti:

                                                       (1.2-15)

Il coefficiente di stipamento assiale per i conduttori di bobina, misurato lungo la direzione parallela all’asse della macchina è:

                                                                                      (1.2-16)

Se si avvolge la bobina con un unico strato (Nst=1)  Ksta vale uno.

1.3  LE EQUAZIONI FONDAMENTALI DELLA MACCHINA

Le formule che regolano il funzionamento e il dimensionamento della macchina vengono ricavate facendo delle ipotesi semplificative che saranno specificate in seguito.   Queste semplificazioni evidenzieranno alcune difformità tra i risultati della progettazione e quelli misurati sulle macchine realizzate. Nella costruzione dell’algoritmo di progettazione si cercherà di ridurre questo divario sfruttando la  rapidità di calcolo degli elaboratori elettronici.

CARATTERISTICA DEI MAGNETI PERMANENTI

I materiali magnetici utilizzati nella produzione industriale sono la ferrite, il Cobalto-Samario e il Neodimio-Ferro-Boro. I magneti sono caratterizzati dalle seguenti caratteristiche:

– Temperatura di Curie (TCurie): la temperatura in cui il materiale perde le sue caratteristiche magnetiche;

–  Temperatura operativa massima (Tmax): la massima temperatura a cui si può lavorare per avere un margine di sicurezza adeguato;

– Campo magnetico coercitivo Hc [kA/m]: è il campo magnetico necessario per annullare l’induzione nel materiale; è quindi un indice per l’utilizzo del materiale sotto campi magnetici esterni;

– Induzione residua Br [Wb/m2]: sarà mostrato in seguito, che questa grandezza è   proporzionale al valore medio dell’induzione al traferro.

La Tabella 6 seguente riassume i valori indicativi di tali grandezze per vari tipi di materiali.

Tabella 6  Caratteristiche di alcuni materiali magnetici

Il materiale più utilizzato per costruire magneti permanenti di alte prestazioni è il Neodimio-Ferro-Boro (Nd-Fe-B). Questa lega è un composto a base di terre rare lavorate per sinterizzazione. Il Nd-Fe-B permette di ottenere valori di energia specifica nettamente superiori anche al Samario Cobalto (Sm-Co).

Mescolato con legante plastico, il Nd-Fe-B offre resistenza e tenacia meccanica elevata. Il raggiungimento di valori di coppia elevati nelle macchine a magneti permanenti e specialmente nelle macchine a disco deriva dalla elevata energia specifica (anche 100 kJ/m3 ) che si è raggiunta con questi magneti di nuova generazione.

  Una smagnetizzazione dovuta ad eventi eccezionali, insieme ad un impiego a temperature elevate, può portare ad una riduzione delle caratteristiche magnetiche. Si deve notare la delicatezza dei magneti al Neodimio-Ferro-Boro, derivante dalla bassa temperatura di Curie.

La curva di smagnetizzazione dei magneti può essere approssimata mediante una retta di equazione:

                                                                        (1.3.1-1)

dove Br≈1.07÷1.3 [T] per il Neodimio-Ferro-Boro. Si ricorda che .

  L’intersezione tra la retta di carico del circuito magnetico e la caratteristica di smagnetizzazione fornisce il punto di lavoro del magnete. Per scegliere il punto di lavoro si potrebbe massimizzare l’energia magnetica specifica sfruttando al massimo il materiale.

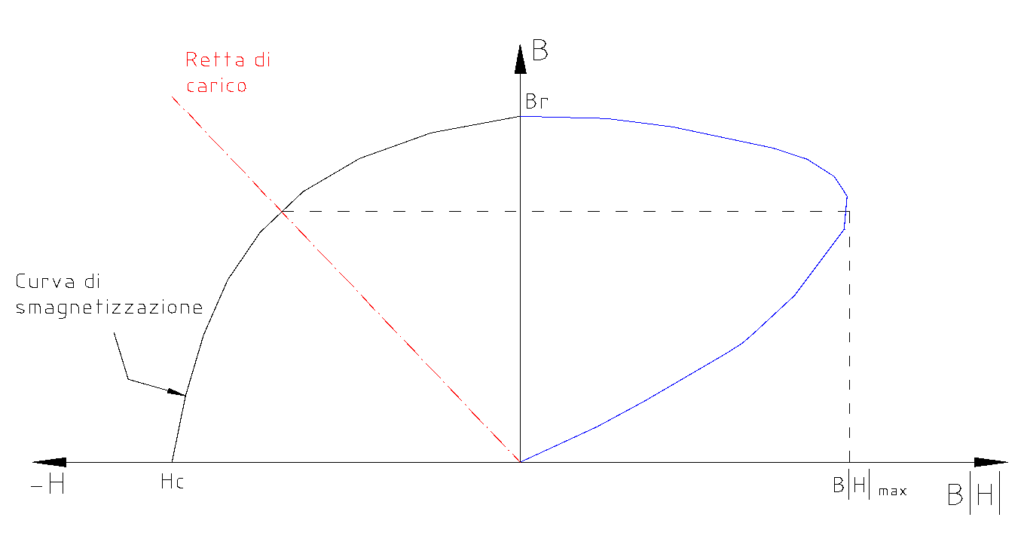
Dalla Figura 11 si possono ricavare i parametri del punto di lavoro per calcolare l’energia specifica:

 

Errore. Non si possono creare oggetti dalla modifica di codici di campo.                                                                              (1.3.1-2)

 

Sostituendo Hm con l’Equazione (1.3.1-1) si trova che l’induzione  Bm che massimizza l’energia specifica Esp,  deve uguagliare l’induzione residua del magnete (Bm = Br/2).

La curva di smagnetizzazione cambia con la temperatura di funzionamento; all’aumentare della temperatura i valori di induzione a parità di campo magnetico sono leggermente minori.

 

1.3.2 STUDIO DEL CAMPO DI INDUZIONE MAGNETICA

Nella Figura 1-8 si osserva una soluzione agli elementi finiti per il campo di induzione sulla geometria minima di una macchina a flusso assiale. Si può notare che alcune linee del campo non si concatenano con le spire delle bobine. Inoltre, a differenza delle ipotesi che si faranno in seguito, le linee del flusso in aria non hanno un andamento perfettamente assiale ma tendono ad aprirsi, perché il ferro di statore è relativamente lontano.

Figura 12  Linee di forza del campo di induzione per un polo di macchina

Per il calcolo del punto di lavoro del magnete si formulano alcune ipotesi semplificative:

1. Il flusso disperso dai magneti è nullo (vedere Figura 1-10a). Tutto il flusso emesso dai magneti entra nel ferro di statore e si concatena con le spire delle bobine.

2. Si considera nulla la riluttanza nello statore e nel rotore e sono quindi nulle le cadute di tensione magnetica nel ferro.

3)  Tutte le formule vengono ricavate sul raggio medio della macchina. Si trascura quindi lo sviluppo in senso radiale della geometria. In pratica, la circonferenza con raggio Rmedio è considerata un baricentro per le interazioni elettromagnetiche che avvengono tra lo statore ed i rotori

Le ipotesi fatte comportano un andamento ad onda quadra del campo al traferro; il flusso di induzione in aria è sempre costante sotto un polo mentre è sempre nullo al di  fuori. Il calcolo della fem effettuato con l’ipotesi 1) fornirà in ogni caso dei risultati maggiori di quelli reali.

La semplificazione del modello non porta a degli errori rilevanti rispetto alla macchina reale. Si deve porre attenzione però, a non portare il ferro oltre il limite di saturazione perché la permeabilità relativa tenderebbe a diminuire e la condizione 2) non sarebbe più soddisfatta.

1.3.3 RELAZIONE TRA SEZIONI DI STATORE E ROTORE

In questo paragrafo si studia il dimensionamento magnetico delle strutture della macchina che sono attraversate dal campo prodotto dai magneti permanenti.

Tenendo conto della Figura 13  Geometria minima con elementi del circuito magneticosi definiscono le seguenti grandezze:

–  Bm Induzione nel magnete permanente, si ricava definendo il punto di lavoro

–  Ba Induzione teorica in aria (traferro magnete – statore ), calcolabile supponendo nulli i flussi dispersi e nulle le cadute di tensione magnetica nel ferro

–  Bfs   Induzione massima nel ferro di statore

–  Bfr Induzione massima nel ferro di rotore

–   Flusso totale uscente da un polo di un magnete attraverso la superficie Sm

–     Flusso disperso da mezzo magnete, ovvero metà del flusso disperso da ciascun polo

–  Flusso che attraversa la sezione Sfs del ferro di statore

–      Flusso che attraversa la sezione Sfr del ferro di statore

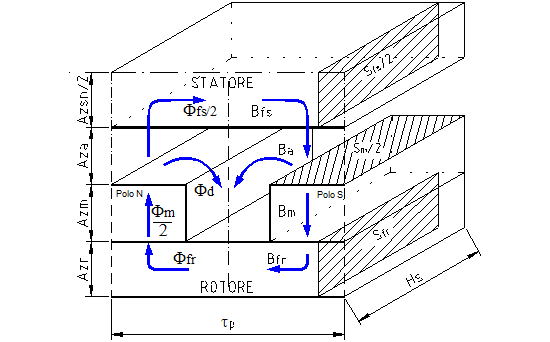
Dalle Figure 1-2, 1-3 e dallo schema della Figura 1-9 si calcola:

–      Il flusso magnetico su un magnete intero:

                                                                          (1.3.3-1)

 

–      Il flusso magnetico nello statore:

                                                                          (1.3.3-2)

–      Il flusso magnetico nel rotore:

                                                                              (1.3.3-3)

    Sulla base della legge di conservazione del flusso, lungo il circuito magnetico deve risultare:

                                                                                          (1.3.3-4)

  Secondo le ipotesi effettuate il flusso disperso si considera nullo e le linee del campo di induzione sono tutte dirette in verso assiale:

                                                                                             (1.3.3-5)

                                                                                                                (1.3.3-6)

                                                                             (1.3.3-7)

   Osservando la Figura 1-9 le formule appena enunciate indicano che il flusso uscente da un polo di macchina sarà uguale al flusso massimo misurato nelle sezioni dello statore che non si trovano sotto i magneti. Nelle sezioni rotoriche il flusso si dimezza.

  Esprimendo il campo di induzione di statore e rotore in funzione del campo al traferro si trova:

                                                                                                 (1.3.3-8)

                                                                                                   (1.3.3-9)

  Quando si vuole sfruttare al massimo il ferro di statore si sceglie un valore di induzione poco al di sotto del ginocchio di saturazione della curva di magnetizzazione. Indicativamente  deve risultare  Bfr= Bfs e quindi Azsn=2 Azr. In conclusione, la sezione di statore deve essere doppia di quella del rotore.

 

1.3.4 SPESSORI DEL TRATTO IN ARIA E DEL MAGNETE

E’ importante stabilire un legame tra le grandezze presenti al traferro, in modo tale che il punto di lavoro dei magneti sia proprio quello desiderato.

Poiché si ritiene nulla la riluttanza nel ferro, dal teorema di circuitazione lungo una linea chiusa che attraversi statore e rotore con un segmento lungo quanto il passo polare  si ricava:

                                                           (1.3.4-1)

La circuitazione è ovviamente nulla se la linea su cui si esegue l’integrale racchiude le tre fasi percorse dalle tre correnti equilibrate.

  Con queste considerazioni si ricava:

                                                                     (1.3.4-2)

vista l’ipotesi di flussi dispersi nulli si può considerare Ba=Bm, per cui:

                                                                          (1.3.4-3)

quindi:

                                                                 (1.3.4-4)

  La massima energia specifica nel magnete si ottiene quando Bm=Br/2. Si conclude che il rapporto Ka = Aza/Azm deve essere vicino all’unità, in altre parole lo spessore del traferro e del magnete devono essere quasi uguali.

   A causa dei flussi dispersi, delle cadute di tensione magnetica e della reazione di indotto, l’induzione Ba=Bm appena calcolata è maggiore di quella reale al traferro.

 

1.3.5 CALCOLO DELLA FORZA ELETTROMOTRICE INDOTTA SU DI UNA SPIRA PUNTIFORME

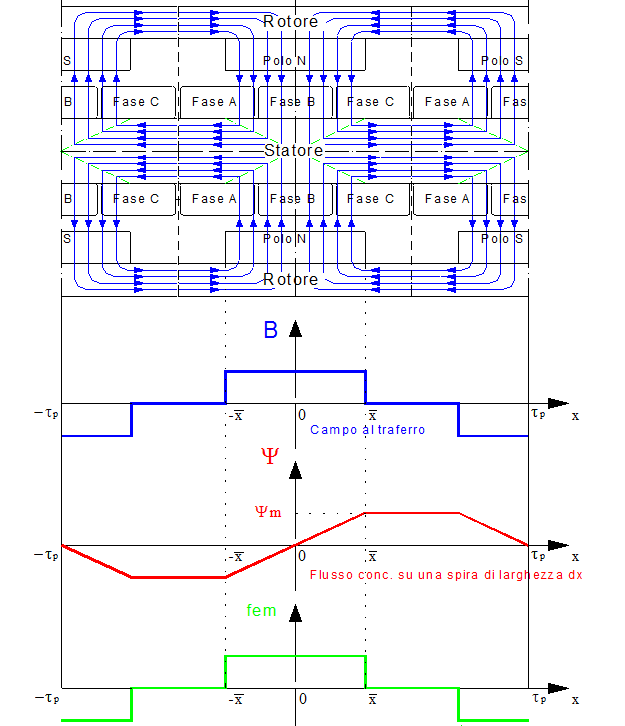
   Per calcolare la forza elettromotrice (fem) indotta in una spira di macchina bisogna determinare l’andamento del flusso di induzione che si concatena con essa.   Con le ipotesi effettuate nel Paragrafo 1.3.2 il flusso magnetico è disegnato nella Figura 1-10.

  Per calcolare la fem bisogna applicare la legge di Faraday che nel caso in esame diventa:

 

(1.3.5-1)

l’ultima uguaglianza vale quando la velocità istantanea è costante.

   Il campo al traferro secondo le ipotesi effettuate al Paragrafo 1.3.2 è disegnato nella Figura 1-10b. Una spira di spessore dx viene investita dal flusso concatenato (vedere Figura 1-10c) che presenta la seguente equazione:

                          per     

                        per                         (1.3.5-2)

                               per     

Dove Hs è lo spessore della corona circolare ().

La derivata di moltiplicata per la velocità periferica fornisce la fem cercata:

                                                     per                  

                        per                                 (1.3.5-3)

                                                     per                   

Nella formula (1.3.5-2) si nota che il flusso concatenato con una spira è uguale alla somma di due flussi ciascuno dei quali è prodotto dal magnete di un rotore.

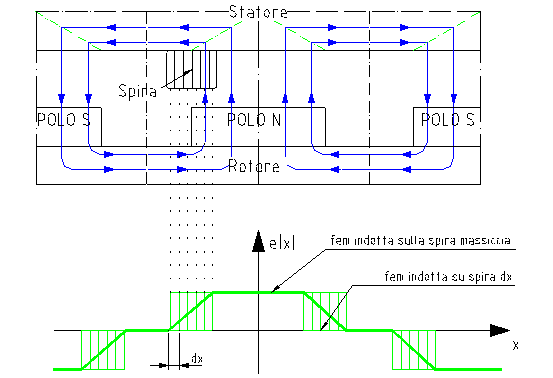
1.3.6 CALCOLO DELLA FEM SU DI UNA SPIRA DI SPESSORE FINITO CON IL METODO ITERATIVO

Nel caso reale le spire della macchina sono massiccie. La fem indotta in una spira  viene calcolata risolvendo il seguente integrale:

                                                  (1.3.6-1)

In pratica, la funzione e(x) può essere determinata dividendo la spira massiccia in nx spire più piccole (con nx elevato). Gli andamenti ad onda quadra delle fem indotte su ogni spira i-esima sono sommati uno sull’altro ed il risultato viene diviso per il numero di divisioni nx. Se nx tende ad infinito si ricava il valore esatto della fem indotta sulla spira massiccia. Un esempio di questo procedimento si trova nella Figura 1-11.

  Più avanti sarà descritto un algoritmo matematico che divide la spira massiccia per calcolare la fem indotta con questo principio, ed arrivare alla soluzione per iterazione.

 

1.3.7 CALCOLO  DELLA FEM SU DI UNA SPIRA DI SPESSORE FINITO CON IL METODO ANALITICO

Viste le ipotesi effettuate al Paragrafo 1.3.2 è possibile calcolare la fem indotta sulla spira massiccia in qualsiasi posizione essa si trovi. In particolare si devono studiare i tre casi della Figura 1-12.

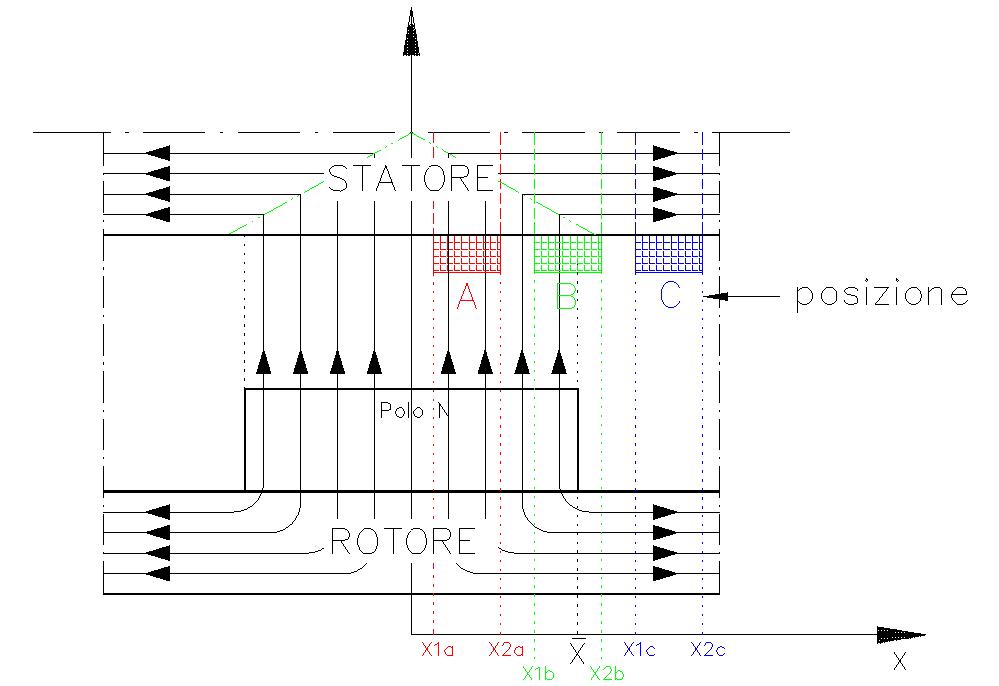
–   Studio della Posizione A della spira: tutta la spira è investita dal flusso magnetico in direzione z.

Il flusso concatenato con la spira vale:

                 (1.3.7-1)

Dove  xm è il punto medio tra X1a ed X2a.

  La fem indotta ha lo stesso valore di quella calcolata per una spira di spessore dx:

                                                                                     (1.3.7-2)

–    Studio della Posizione C: il flusso concatenato con la spira non varia lungo δ

                                                                                (1.3.7-3)

La derivata del flusso e quindi la fem è sempre nulla in questo settore ()

– Studio della Posizione B:  la spira  è investita  parzialmente dal flusso in direzione z.

L’integrale del flusso è composto da due funzioni: una variabile linearmente con x e l’altra costante.

             

           

                  (1.3.7-4)

La fem indotta vale:

                                                 (1.3.7-5)

Osservando la Formula 1.3.7-5 si può costatare come il valore della fem equivale alla media algebrica delle fem indotte in due conduttori fittizi in parallelo che costituiscono la spira. La media deve essere pesata rispetto allo spessore δ. I due conduttori fittizi sono i seguenti: il primo,   posizionato tra l’ascissa ed dove viene indotta una fem pari a ; il secondo posto tra e presenta una fem  indotta nulla.

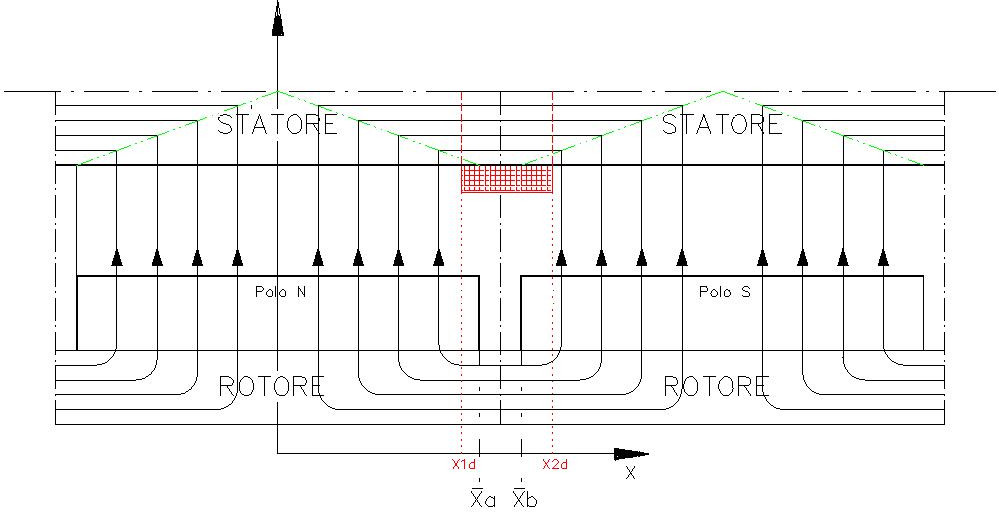
Oltre a queste tre posizioni appena studiate si può presentare un’altra configurazione se la geometria dello spazio polare è quella della Figura 1-13. In questo caso la spira di spessore finito è posizionata  sotto due poli magnetici.  Si può comunque dimostrare che il calcolo della fem anche in questo caso si può effettuare dividendo la spira in porzioni di spessore Δxi per calcolare la fem indotta su ciascuno di essi. In seguito, si deve effettuare la media algebrica delle fem pesata rispetto allo spessore.

1.4  CALCOLO DELLA COPPIA

  Nella macchina a flusso assiale, la produzione di coppia tra i due rotori e lo statore avviene mediante l’interazione elettromagnetica tra la componente normale del campo di induzione magnetica al traferro e la corrente negli avvolgimenti dello statore. La forza tangenziale (dF(t)=I(t) dsxB(t)) che le due strutture si scambiano risulta  proporzionale proprio a queste due grandezze e alla lunghezza dei lati attivi dei conduttori. La presenza di due rotori affacciati sui lati attivi delle bobine di macchina, permette di sfruttare ciascuna spira   per due volte.  Infatti, due lati attivi di una spira, percorsi da correnti opposte ma che si trovano sotto due poli magnetici identici verranno sottoposti a due forze di verso concorde.

La coppia elettromagnetica può quindi essere calcolata come il momento risultante prodotto da queste forze tangenziali.

Il calcolo della coppia deve essere implementato in un algoritmo, è possibile risalire al valore istantaneo di questa grandezza applicando l’equazione di conservazione dell’energia. Di seguito viene riportata la formulazione di questo principio:

                                                    (1.4-1)

   L’equazione 1.4-1 indica semplicemente che l’energia elettrica prodotta nel tempo infinitesimo dt si trasforma in:

– () Lavoro meccanico dato dal prodotto tra la coppia istantanea e l’angolo di rotazione infinitesimo.

– ( ) Variazione di energia cinetica delle masse rotanti della macchina

– () Calore dissipato dalla macchina nel tempo dt

– () Variazione di energia magnetica

L’energia magnetica in pratica risulta tutta localizzata nel traferro della macchina. Quando i magneti sono in movimento in un punto qualunque del traferro, l’energia magnetica specifica dWm=H . dB è variabile nel tempo con una legge periodica.   Tuttavia  l’integrale nel volume del traferro di dWm rimane costante.  Si conclude che la variazione di energia magnetica dEm nella macchina a flusso assiale può essere considerata nulla.

Sviluppando la Formula 1.4-1 si ricava l’andamento della coppia:

                                                    (1.4-2)

Indicando con Ploss la potenza termica perduta l’equazione 1.4-2 in condizioni di velocità angolare costante diventa:

                                                                (1.4-3)

Analizzando quest’ultima funzione, si rileva che il termine () non   è dipendente dalla velocità della macchina perché come visto nei paragrafi precedenti la fem è direttamente proporzionale alla velocità angolare.  In pratica, all’aumentare della velocità la coppia cresce perché tende a diminuire il secondo termine dovuto alle perdite ( Ploss / ). Purtroppo nelle macchine a disco utilizzate per azionamenti di trazione  questo andamento non è favorevole perché le coppie più alte servirebbero quando il veicolo si trova in fase di accelerazione alle basse velocità.

  Invece di utilizzare l’Equazione 1.4-3 su una bobina reale di Ncb spire la si applica ottenendo gli stessi risultati sulla stessa bobina con una sola spira ideale. Si può, infatti, dimostrare che questo modello matematico fornisce gli stessi valori con dei vantaggi sostanziali:

1)  I calcoli  sono più semplici e veloci.

2) Si rimanda ad una successiva fase di affinamento la scelta della forma e della dimensione del conduttore con il conseguente stipamento dello stesso.

  Dato un valore indicativo per la densità superficiale di corrente Jeff (nel funzionamento a regime deve risultare Jeff  Jmax; vedere Paragrafo 1.9) e fissata la geometria della macchina si può ricavare la corrente totale che attraversa una bobina nel tempo:

                                                  (1.4-4)

Il calcolo di I(t) viene effettuato portando fuori J(t) dall’integrale di superficie; si suppone cioè che la corrente si disponga in maniera uniforme sulla sezione del conduttore.

       Con il simbolo Sbob si indica la superficie disponibile per ogni bobina per l’avvolgimento dei conduttori sullo statore. Il valore di questa superficie è vincolato dalla geometria della macchina: se con Rint  si indica il raggio interno della macchina, la superficie Sbob vale:

                                                              (1.4-5)

Rispetto alla soluzione finale, la superficie Scu calcolata con questo criterio può portare ad errori in eccesso provocati sia dalla presenza nella superficie dello strato isolante dei conduttori, sia dallo spazio lasciato inutilizzato al momento dell’avvolgimento di conduttori con sezione unificata.

  La scelta in questa fase del valore della Jeff non richiederà correzioni se le verifiche termiche e di smagnetizzazione daranno esito positivo. Si rimandano queste problematiche ad una fase di successivo affinamento.

  Il calcolo di I(t) viene effettuato portando fuori J(t) dall’integrale di superficie; si suppone cioè che la corrente si disponga in maniera uniforme sulla sezione del conduttore. La potenza perduta (calore nell’unità di tempo da smaltire) risulta essere la somma di vari addendi:

 

                                                                    (1.4-6)

–    Perdite nel rame per effetto Joule

–      Perdite addizionali nel rame per correnti parassite

–        Perdite nel ferro per isteresi magnetica

–       Perdite per correnti parassite

       Gli ultimi tre tipi di perdite si presentano anche se la macchina funziona a vuoto: in questo caso, il motore assorbirà l’energia necessaria per alimentare queste perdite e quella per vincere gli attriti meccanici.

     L’andamento temporale della coppia elettromagnetica può essere determinato sommando i contributi delle tre fasi e moltiplicando per il numero di poli.

1.5  CONVERTITORI  E FORMA  D’ONDA  DELLA  CORRENTE

  I motori a flusso assiale sono alimentati con convertitori a tensione impressa o a corrente impressa (Voltage-Stiff Inverter VSI e Current-Stif Inverter CFI) [5].

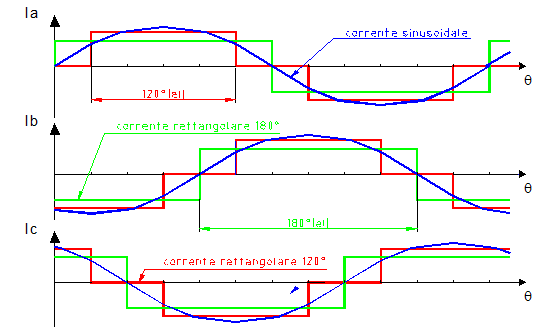
  In generale la corrente di fase in questa macchina può avere tre forme d’onda:

–     Sinusoidale               (motore alimentato da Inverter)

• Rettangolare a 120° (generatori o motori collegati a sistemi di elettronica di

      potenza)

–     Rettangolare a 180°

  I primi due tipi di forme d’onda danno origine ad un sistema di correnti trifasi equilibrato. In questo caso non c’è bisogno di collegare anche il neutro con le bobine della macchina. Le correnti trifasi rettangolari a 180° invece, non formano un sistema equilibrato.

  Nel primo caso oltre all’armonica fondamentale di corrente si presentano anche altre armoniche di ordine superiore. Il parametro THD (Total Harmonic Distorsion ) assume valori più o meno elevati a seconda del tipo di Inverter e della frequenza di accensione e spegnimento degli Switches.

  In un generatore l’onda perfettamente rettangolare si otterrebbe se a valle del raddrizzatore ci fosse un generatore di corrente costante e se l’induttanza di macchina fosse nulla.

  Nella realtà ci si avvicina a queste condizioni perché vengono montate induttanze  di livellamento che servono a spianare la corrente  ed inoltre l’induttanza di macchina è bassa a causa dell’elevato traferro.

In questo tipo di macchina è utile introdurre una grandezza chiamata densità lineare di corrente Jl  [A/m] definita da questo rapporto:

                                                                                      (1.5-1)

La grandezza Jl misura l’influenza della geometria della macchina sul dimensionamento elettrico.

1.6 LE PERDITE NEL RAME

Si è visto nel Paragrafo 1.4 che nel rame degli avvolgimenti si instaurano  le seguenti perdite di energia:

1)    Perdite nel rame per effetto Joule

2)    Perdite addizionali nel rame per correnti parassite

  Normalmente la macchina a flusso assiale lavora a frequenze minori di 100 Hz. Si può quindi affermare che le perdite per effetto Joule sono le più rilevanti. Il simbolo Rf  è la resistenza di fase calcolabile con la formula:

                                                                                                  (1.6-1)

si è indicato con: Ltf  la lunghezza totale del conduttore di fase; Scu  la sezione.

La  resistività ρcu (T) del rame dipende  dalla   temperatura di funzionamento (Tf [°C]):

                                                         (1.6-2)

Osservando la Figura 1-6 la lunghezza media Lsp di ciascuna spira dell’avvolgimento può essere valutata con l’espressione:

                                                  (1.6-3)

Supponendo di collegare, in serie tutte le spire di fase e considerando che per ciascuna fase vi sono Nc/3 spire complete si trova:

                                                                                            (1.6-4)

per cui:

                                                                      (1.6-5)

Scu è la sezione del conduttore che costituisce la spira.

  La potenza perduta per effetto Joule può essere calcolata in funzione della densità lineare di corrente Jl:

                                                                         (1.6-6)

  Nel rame ci sono altre perdite provocate dalle correnti parassite. I conduttori, infatti, sono tagliati dal campo magnetico variabile nel traferro.

  Le perdite addizionali possono essere stimate per unità di volume [W/m3] con la formula empirica:

                                                                                      (1.6-7)

con il simbolo  sc si indica lo spessore in direzione trasversale al flusso dei conduttori; k è un coefficiente empirico uguale a 32 o 24 rispettivamente per conduttori di sezione circolare o a piattina. Durante il funzionamento, le perdite addizionali variano con il quadrato della velocità o della frequenza (). Per ridurre le perdite addizionali si avvolgono i conduttori a piattina affiancandoli sul lato maggiore.

 

1.7 LE PERDITE NEL FERRO

Nello statore della macchina sono localizzate due diversi tipi di perdite:

1) : perdite per isteresi magnetica, causate da fenomeni d’attrito nella struttura cristallina del materiale ferromagnetico. Se il flusso varia ciclicamente con frequenza pari ad f [Hz], le perdite per isteresi per unità di massa valgono:

             = Kis · f · BMα        [W/kg]                                                                  (1.7-1)

dove Kis è una costante che dipende dalla natura del materiale ferromagnetico, BM è il valore massimo dell’induzione elettromagnetica, l’esponente α vale 1,6 se BM<1 [T], 2 se BM1 [T].

2) : perdite per correnti parassite, causate dalle correnti parassite che si instaurano nel materiale essendo questo conduttore. Tali correnti parassite sono sostenute dalle fem indotte nel materiale ferromagnetico tagliato dal flusso di induzione variabile. Se il flusso varia ciclicamente con frequenza pari ad f [Hz], le perdite per correnti parassite in ciascun [kg] peso valgono:

 

         = Kcp · (Kf · f · BM)2     [W/kg]                                                               (1.7-2)

 

dove Kcp è una costante che dipende dalla natura del materiale ferromagnetico e dallo spessore dei singoli lamierini, Kf è il fattore di forma dell’onda di variazione del flusso nel tempo (Kf  vale 1,111 nel caso di variazioni perfettamente sinusoidali).

  Le due perdite sopra elencate sono sommate per ottenere le perdite complessive nel ferro. I costruttori di materiali ferromagnetici forniscono un dato tecnico molto importante, noto come cifra specifica di perdita cp. La cifra specifica di perdita per un dato materiale ferromagnetico rappresenta le perdite complessive nel ferro riferite ad 1 [kg] di materiale sottoposto ad un flusso magnetico variabile con frequenza di 50 [Hz], di forma d’onda sinusoidale ed una induzione massima di 1 [Wb/m2]. Nota la cifra specifica di perdita, le perdite nel ferro sono ricavabili con l’espressione empirica:

 

                     [W]                                                         (1.7-3)

 

è possibile determinare le perdite nel ferro nel caso in cui si abbia una induzione massima pari a BM [Wb/ m2], una frequenza pari ad f [Hz] ed un peso del ferro dello statore  pari a Mfs [kg].

 

1.8  STUDIO DEL CARICO TERMICO DEL MOTORE

Le perdite elettriche delle macchine sono localizzate nello statore. Quando la macchina lavora a velocità costante, la potenza elettrica che le viene fornita si trasforma in potenza meccanica ed in potenza termica, cioè calore nell’unità di tempo. In condizioni di regime termico, il calore prodotto non innalza ulteriormente la temperatura degli elementi ma viene tutto dissipato all’esterno.

Il problema che si deve affrontare riguarda il calcolo della temperatura di funzionamento che la macchina può raggiungere in determinate condizioni. Si presentano, infatti, dei limiti sulla temperatura di funzionamento dati dalla necessità di non danneggiare o ridurre la vita media degli isolamenti dei conduttori nel pacco statorico.

La sorgente di calore è localizzata sullo statore. I rotori raggiungeranno a regime una temperatura più bassa dello statore. I magneti permanenti però, devono essere lo stesso salvaguardati non solo perchè il loro prezzo incide in maniera rilevante sul costo totale della macchina, ma anche perché una loro smagnetizzazione implica un degrado delle caratteristiche operative.

Il calore è trasportato per conduzione dai materiali che costituiscono lo statore, e tende ad essere dissipato all’esterno riscaldando l’aria che lambisce la corona circolare. Lo scambio di potenza termica con l’aria interessa tutta la superficie dello statore, in special modo lo strato di resina nel quale è affogato tutto il pacco statorico.

Il coefficiente di convezione che regola lo scambio di calore tra l’aria e lo statore tende ad aumentare con la velocità dell’aria.

Nella macchina a flusso assiale il raffreddamento avviene grazie alla circolazione forzata che l’aria subisce nel traferro in direzione radiale. I profili laterali dei magneti assumono la stessa funzione della palettatura di un ventilatore centrifugo.  Il volume d’aria presente nelle cavità tra due magneti vicini, viene portato in rotazione dai rotori e tende a spostarsi all’esterno a causa dell’accelerazione centrifuga. La traiettoria del flusso d’aria e quindi la velocità sarà data dalla somma di due componenti: quella tangenziale e quella radiale.

  Durante il funzionamento il 90% delle perdite sono prodotte dagli avvolgimenti in rame. Le bobine di macchina, dal punto di vista termico, possono essere considerate un corpo omogeneo e compatto, che in condizioni di regime si trova tutto alla stessa temperatura Tf. La conducibilità termica del rame è, infatti, molto elevata, mentre lo strato di smalto interposto tra le spire è sempre molto sottile (ss=0.040.05 mm). E’ quindi corretto considerare nulli i gradienti di temperatura all’interno dell’avvolgimento.

In tutti i problemi di questo genere, la temperatura finale della macchina dipende strettamente dalla temperatura ambiente. Data la macchina ciò che si può calcolare e la sovratemperatura T definita in questo modo:

 

                                                                                                           (1.8-1)

 

  La sovratemperatura  T deve essere tale da mantenere  la temperatura Tf al di sotto della temperatura Tmax ammissibile per i materiali isolanti dell’avvolgimento.

  La potenza perduta Ploss definita nella Formula 1.4-6,   sarà come già scritto la somma delle perdite nel rame e nel ferro. Nella Figura 1-15, è disegnato lo schema per la dissipazione del calore della macchina. Con i vettori si evidenziano la posizione delle sorgenti di calore ed il percorso dei flussi termici. In pratica, le perdite di calore sono dissipate all’esterno nella zona del traferro della macchina.

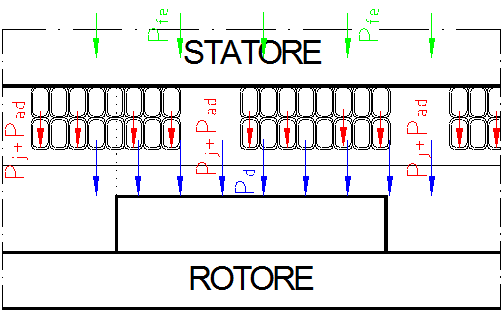
La superficie totale Ssc di scambio termico con l’esterno, nel caso di statore completamente resinato può assumersi pari a:

 

                                                                                     (1.8-2)

 

questa superficie non è altro che la somma delle due superfici di statore affacciate ai traferri. Si trascura quindi il contributo delle testate alla dissipazione di calore. Questa ipotesi cautelativa compensa in parte gli errori dovuti all’aver considerato l’intero avvolgimento come un corpo omogeneo di capacità termica infinita. In realtà la superficie di statore riscaldata dall’avvolgimento è maggiore e si estende circa per tutta l’altezza Hb delle bobine.

Nella Figura 20 è rappresentato un semplice modello elettrico equivalente al circuito termico in esame: il salto di temperatura equivale alla caduta di tensione; la sorgente di calore viene considerata come un generatore di corrente; infine, le resistenze termiche sono equivalenti a quelle elettriche.

Figura 20  Schema elettrico equivalente di un modello termico semplificato

 

  I simboli della Figura hanno il seguente significato:

 

   Resistenza termica dello strato di smalto isolante sui conduttori

   Resistenza termica offerta dallo strato di resina protettiva

    Resistenza termica dovuta all’adduzione superficiale tra resina e aria

 

Nel circuito in esame non si considera la resistenza termica dell’avvolgimento in rame perchè è di tre ordini di grandezza più piccola delle altre.

La conducibilità termica s dello smalto isolante varia a seconda della classe di isolamento (Tabella 1-2 ). Il simbolo s vale s=0.10.25 [W K-1m-1]; la conducibilità termica r della resina protettiva può assumersi pari a r=0.5 0.8  [W K-1m-1].

 

Tabella 7  Valori di conducibilità termica caratteristici per alcuni  isolamenti

Tabella 1-2

Più importante e complessa e la determinazione del coefficiente di adduzione  (in pratica coincidente con il coefficiente di convezione cf) il cui valore dipende sensibilmente dalla velocità va del flusso d’aria refrigerante che lambisce la superficie di statore.

Uno studio più approfondito del fenomeno di convezione richiede di conoscere l’esatta configurazione geometrica dello spazio al traferro. Il calcolo preciso di  è possibile solo in questa fase della progettazione.

Le resistenze Rts, Rtr, Rta  definite in precedenza sono disposte in serie e sottoposte al salto termico totale T; attraverso di esse fluisce la potenza dissipata Pd (Figura 1-16)

 

                                                                                               (1.8-3)

 

In condizioni di equilibrio termico Ploss=Pd, perciò dalla relazione precedente si ricava:

 

                                                                 (1.8-4)

 

essendo Crt [K m2 / W] il coefficiente globale di resistenza termica:

 

                                                                                                   (1.8-5)

 

Trascurando le perdite nel ferro e le perdite addizionali nel rame la densità superficiale di corrente massima Jmax, ammissibile per non surriscaldare l’avvolgimento può essere calcolata con la formula seguente:

 

                                                                             (1.8-6)

 

Considerando cautelativamente   si può calcolare la densità lineare di corrente Jlmax:

 

                                                                      (1.8-7)

 

Se nel problema termico vengono prese in considerazione tutte le perdite della macchina ( le perdite Ploss  vengono calcolate con la Formula 1.4-6 ) allora la densità superficiale di corrente  può essere espressa in questo modo:

 

                      (1.8-8)

 

Queste due grandezze non dovrebbero essere superate in condizioni di regime. Se invece la macchina si trova in un certo istante ad una temperatura inferiore a Tf può subire delle sovracorrenti la cui intensità e durata sono legate alla capacità termica della massa statorica, o per meglio dire alla costante di tempo termica del motore.

 

1.9  STUDIO DELLE SOLLECITAZIONI MECCANICHE SUI ROTORI

 

I due dischi rotorici sono sottoposti alle forze di attrazione esistenti tra i magneti, fissati sulla loro superficie, ed il nucleo statorico. Tali forze si traducono in una sollecitazione a flessione dei dischi che tenderanno ad avvicinarsi allo statore. Ovviamente, la risultante delle sollecitazioni assiali agenti sullo statore, è nulla perchè le forze di attrazione dei due rotori si bilanciano.

Le sollecitazioni in gioco potrebbero provocare un incurvamento della struttura rotorica, con il rischio che i magneti comincino a strisciare sulla superficie resinata del pacco statorico. Il problema consiste nel calcolare il valore delle forze di attrazione per dimensionare lo spessore del disco rotorico in modo che il materiale rimanga nel campo elastico senza subire deformazioni permanenti. Inoltre, è necessario che nel campo elastico il materiale non subisca frecce di inflessione che annullino lo spazio del traferro in aria.

Il calcolo delle forze è effettuato applicando il principio dei lavori virtuali. Come già detto l’energia magnetica prodotta da un magnete può essere considerata tutta immagazzinata nel traferro. L’energia magnetica vale quindi:

 

                                                                          (1.9-1)

 

Dove con Vs si indica il volume occupato dal traferro sotto un polo di macchina              ( ). Come valore di induzione in aria, si considera cautelativamente l’induzione teorica Ba rimanendo in favore di sicurezza.

La forza di attrazione tra un magnete ed il ferro di statore può essere così calcolata:

 

                                                                                      (1.9-2)

 

La forza totale Frot esercitata sulle piastre circolari di rotore viene ottenuta moltiplicando Fmg per il numero di magneti p montati sul rotore.

 

                                                                                        (1.9-3)

Il calcolo della deformazione può essere condotto considerando il disco rotorico di acciaio come una piastra anulare di raggio interno Rmin e raggio esterno Rest incastrata in corrispondenza della circonferenza interna e sottoposta ad un carico uniformemente distribuito lungo la circonferenza esterna e concentrato in senso radiale. Vista la Figura 1-17 si sposta la forza P applicata sul raggio medio considerando una forza Pest che produce lo stesso momento flettente:

                                                                                                         (1.9-4)

  In questo caso per il calcolo della freccia di inflessione si può utilizzare la formula:

 

                                                                                                   (1.9-5)

 

essendo: fmax [mm] la freccia valutata sulla circonferenza di raggio Rest;  E [kg/mm2] il modulo di Young del materiale  (per l’acciaio E=21000 [kg/mm2]); k1 è un coefficiente  dipendente dal rapporto Rest/Rmin  ( K1= 0.3  0.7 ).

Figura 21  Schema di un disco rotorico sottoposto ad una forza di inflessione

 

Il calcolo meccanico non è elementare e varia a seconda del collegamento dei rotori  con l’albero del motore. Occorre anche tenere in conto che la presenza dei fori di ventilazione, determina una diminuzione della resistenza a flessione dei dischi. Per ricondursi al caso di disco munito di un solo foro centrale, si deve ricorrere al metodo della rigidezza equivalente, in altre parole si deve sostituire la struttura reale con una struttura equivalente priva di fori e di minore spessore, in grado di presentare la stessa resistenza meccanica alla sollecitazione in esame.

In conclusione, il calcolo a flessione dei dischi rotorici può essere difficilmente affidato ad un algoritmo di calcolo perché la complessità del problema è alta ed inoltre l’affidabilità dei risultati non sarebbe garantita.

1.10   CALCOLO DEL RENDIMENTO DEL MOTORE

 

Calcolata la coppia media di macchina e conoscendo la velocità angolare  si può risalire alla potenza meccanica della macchina:

 

                                                                                         (1.10-1)

 

Una piccola quota parte di questa potenza viene comunque perduta per gli attriti meccanici all’albero.

La potenza dissipata Ploss è già stata definita nel Paragrafo 1.4. Il rendimento del motore potrà essere definito come:

 

                                                                                                (1.10-2)

 

Dove con Pt si è definita la potenza totale fornita dal convertitore.

Una volta specificato il convertitore ed il suo rendimento con si potrà calcolare il rendimento globale dell’azionamento elettrico.

 

                                                                                                         (1.10-3)

 

1.11 CALCOLO DEL PESO DELLA MACCHINA

 

Il peso della macchina viene calcolato al netto del peso dell’albero, dei cuscinetti, del mozzo, e degli elementi di supporto perché questi elementi non possono essere definiti a priori. Le dimensioni dei rotori calcolate evitando che il ferro vada in saturazione potrebbero essere ottimistiche; infatti le due strutture sono sottoposte ad una sollecitazione a flessione provocata dalla forza di attrazione dei magneti con lo statore. Il calcolo meccanico della deformazione potrebbe portare ad una maggiorazione dello spessore del disco rotorico oppure ad una variazione del collegamento tra il disco e la flangia calettata sull’albero.

Queste problematiche non possono essere risolte da un algoritmo ma devono essere affrontate di volta in volta. Per avere un ordine di grandezza della coppia specifica si effettuano comunque i seguenti calcoli:

 

Peso del ferro di statore:

                     con                     (1.11-1)

Peso del rame dei conduttori:

                                            (1.11-2)

Peso indicativo di un rotore:

                                                    (1.11-3)

Peso dei magneti:

                                     (1.11-4)

 

Si indica con  Mtpa dei materiali attivi  (ferro, magneti, rame) :

 

                                                                         (1.11-5)

 

si può definire la coppia specifica Tsp per unità di massa:

 

                                                                                                             (1.11-6)

 

Sebbene Mtpa sia ben al di sotto del reale peso della macchina il parametro Tsp è significativo nel descrivere la qualità di un motore.

 

63651088. 1.12  STRUTTURA E MATERIALI DELLO STATORE

 

Come specificato nel Paragrafo 1.2 lo statore viene costruito avvolgendo a spirale del lamierino del tipo in Tabella 1-3. Può essere utile tagliare in due parti il nucleo di statore affinché si possano infilare le bobine già preparate in separata sede. Per proteggere lo smalto dei conduttori dal contatto con i lamierini taglienti dello statore, il nucleo viene preventivamente coperto da un nastro adesivo.

Tabella 8  Caratteristiche di un materiale ferromagnetico di statore

Tabella 1-3     Caratteristiche di un materiale ferromagnetico di statore

 

Dopo aver provveduto a riassemblare lo statore ed aver effettuato le connessioni delle bobine secondo le specifiche di progetto si ricopre la struttura con resine epossidiche del tipo in Tabella 9.

 

Tabella 9 Caratteristiche di una resina isolante di statore

 

In questa fase bisogna posare lo statore in uno stampo cilindrico che poi viene riempito dalla colata di resina. Questa operazione è necessaria per rendere lo statore più rigido e più resistente alle sollecitazioni meccaniche alle quali soprattutto i conduttori sono sottoposti. La resina offre, infatti, ottima resistenza alle sollecitazioni meccaniche: nella resina si possono ad esempio ricavare i fori attraverso i quali passano i bulloni che fissano lo statore al telaio della macchina.

 

1.13 COLLEGAMENTO DELLE BOBINE

 

Le connessioni tra le bobine di fase vengono realizzate sulla circonferenza interna di statore: i terminali delle bobine sono saldati ad alcuni conduttori ausiliari. Per portare all’esterno i conduttori si realizza ‘mezza spira’ in più o in meno per l’ultima bobina di ogni fase.

Nel caso si prevedano più di tre morsetti esterni, i collegamenti tra i terminali di fase possono essere modificati in un secondo momento, per adattare la macchina al livello di tensione desiderato. Alcuni possibili collegamenti sono schematizzati in Figura.