Analisi FE | Modellazione Magneti Permanenti

PROGETTO DI MACCHINE SINCRONE A FLUSSO ASSIALE A MAGNETI PERMANENTI. ANALISI 3D AGLI ELEMENTI FINITI. POTENZIALE SCALARE

Per il progetto accurato della macchina a flusso assiale viene utilizzato un algoritmo numerico (AFPMs). Il modello matematico permette di calcolare le grandezze di macchina attraverso l’implementazione di un algoritmo tridimensionale agli elementi finiti.

La formulazione agli elementi finiti prevede l’uso di un potenziale scalare. Gli algoritmi prodotti permettono una valutazione accurata delle principali grandezze di macchina come il flusso concatenato, la fem indotta ed il campo di induzione magnetica al traferro.

Come in tutte le macchine elettriche il campo di induzione magnetica risulta essere il mezzo per la conversione di energia. Una computazione accurata del campo magnetico è di conseguenza essenziale per una predizione realistica delle prestazioni in fase di progettazione numerica.

Le tecniche di approccio progettuale per la determinazione della soluzione di campo, sono generalmente ristrette a geometrie bidimensionali semplificate.

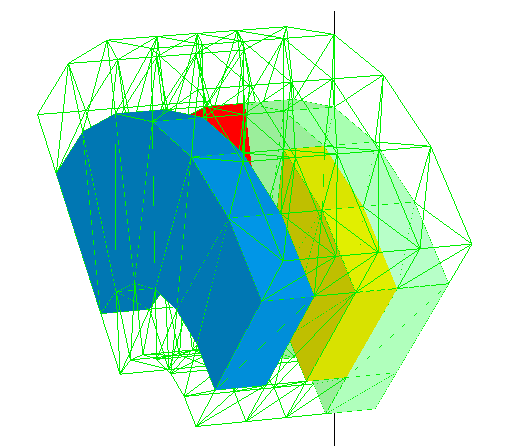
Per raffinare la soluzione di campo la struttura costruita appartiene solo a mezza macchina: in figura viene rappresentato un rotore e solo mezzo statore (riportato in blu). Due mezzi magneti permanenti sono montati sul disco rotorico.

Un analisi FEM 3D risulta essere di notevole interesse per la macchina AFPM, perché la configurazione geometrica e di conseguenza, le grandezze elettriche di macchina possono cambiare notevolmente da una sezione radiale all’altra.

Le analisi FEM 2D sono generalmente limitate a superfici radiali costanti. Su queste superfici si può implementare facilmente un potenziale vettore convenzionale. Per un analisi 3D la difficoltà maggiore consiste nel definire per ogni nodo della mesh un potenziale vettore costituito da tre componenti cartesiane. Sia in fase di implementazione, che di risoluzione, che di post-processing il peso computazionale del problema risulta essere triplicato.

Una distribuzione di campo 3D ottenuta attraverso una funzione potenziale scalare MSP è stata ottenuta utilizzando un’analisi agli elementi finiti diversa dalle precedenti. In questo modo ogni possibile configurazione dei magneti permanenti (non necessariamente rettangolari o circolari) può essere analizzata in dettaglio.

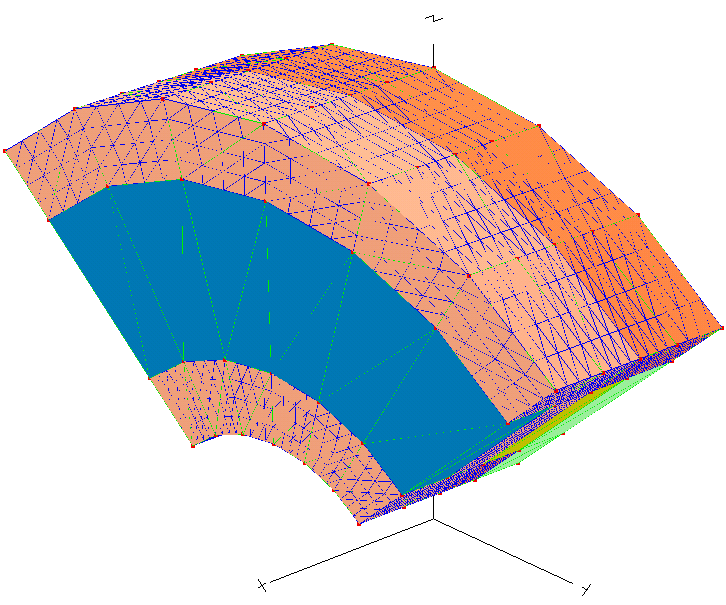
In Figura 7-1 è mostrata una struttura 3D elementare di un polo elettrico di una AFPM. La struttura geometrica 3D non è ancora la minima possibile dato che in condizioni di funzionamento a vuoto è possibile anche limitare l’analisi a mezzo polo di macchina.

Comunque in fase sperimentale si è preferito studiare un polo di macchina perché risulta essere molto vantaggioso analizzare la soluzione fornita dal programma verificando immediatamente la simmetria della soluzione di campo rispetto ad all’asse di simmetria.

La soluzione del MSP è stata analizzata nel post-processing per calcolare il flusso concatenato con gli avvolgimenti di macchina. Per determinare la forma d’onda della fem indotta in condizioni di funzionamento a vuoto, prendendo in considerazione l’intero contenuto armonico, bisogna analizzare il flusso concatenato per ogni posizione angolare tra lo statore ed il disco rotorico della macchina. Anche in post-processing è stato sviluppato un buon algoritmo che permette di calcolare il flusso concatenato in una bobina massiccia di macchina, in ogni posizione angolare.

Figura – Struttura geometrica del modello FEM in fase di refinement

Il programma implementato permette di determinare il flusso concatenato in ogni posizione utilizzando una sola soluzione agli elementi finiti. E’ inoltre possibile analizzare automaticamente le possibili variazioni delle performance della macchina. Questo è particolarmente utile ad esempio durante analisi parametriche o processi di ottimizzazione numerica.

SOLUZIONE AGLI ELEMENTI FINITI IN CONDIZIONI DI FUNZIONAMENTO A VUOTO DELLA MACCHINA (CORRENTE NULLA)

Dato che il rotore del gradiente di una funzione scalare è identicamente nullo $(\overrightarrow{\bigtriangledown} \times \overrightarrow{\bigtriangledown} \varphi )$ ,condizione necessaria affinché un vettore $\overrightarrow{B_{0}}$ sia conservativo (cioè sia esprimibile come gradiente di un potenziale scalare $\varphi$ , condizione necessaria affinché un vettore $\overrightarrow{B_{0}}$ : $\overrightarrow{B_{0}} = -\overrightarrow{\bigtriangledown} \varphi$ è che il suo rotore sia nullo ( $(\overrightarrow{\bigtriangledown} \times \overrightarrow{\bigtriangledown} \varphi = \overrightarrow{\bigtriangledown} \times \overrightarrow{B} = 0)$ . Poiché il campo magnetostatico $\overrightarrow{B_{0}}$ non gode di questa proprietà ( è in generale diverso da zero), esso non è dunque in generale conservativo.

Tuttavia, la densità di corrente $\overrightarrow{J}$ è di solito diversa da zero solo in porzioni assai limitate dello spazio (nelle porzioni di spazio occupate da conduttori, spesso rappresentati da semplici fili metallici). Ci si chiede allora se in tutto lo spazio restante, in cui essendo nulla la densità $\overrightarrow{J}$ è $\overrightarrow{\bigtriangledown} \times \overrightarrow{B} = 0$ , il campo $\overrightarrow{B_{0}}$ sia conservativo; cioè se sia esprimibile come gradiente di un potenziale scalare (che nel sistema S.I. si misurerà in Tesla

per metro). In termini matematici, ciò è come chiedersi se la condizione:

$\overrightarrow{\bigtriangledown} \times \overrightarrow{B_{0}} = 0$ ( 71 )

per l’esistenza di un potenziale scalare monodromo oltre che necessaria sia anche sufficiente per l’esistenza di una funzione monodroma (cioè definita a meno di una eventuale costante che abbia però lo stesso valore in ogni posizione) di cui $\overrightarrow{B_{0}}$ sia il gradiente (per omogeneità con il potenziale elettrostatico, si preferisce in realtà cambiare segno):

$\overrightarrow{B_{0}} = -\overrightarrow{\bigtriangledown} \varphi$

Nel caso particolare di una regione 2D o 3D libera da correnti elettriche ( ), l’equazione di Maxwell degenera in un caso di irrotazionalità

$\overrightarrow{\bigtriangledown } \times \overrightarrow{H} = 0$

Questa caso permette di asserire che per il campo magnetico $\overrightarrow{H}$ esiste un potenziale scalare P tale che:

$\overrightarrow{H} = -\overrightarrow{\bigtriangledown} P = 0$

L’equazione di Maxwell $\overrightarrow{\bigtriangledown}\overrightarrow{B} = 0$ può essere riscritta per mezzo di una equazione costitutiva $\overrightarrow{B}=\mu \overrightarrow{H}$ , come

Questa formulazione è in pratica una versione non lineare dell’equazione di Laplace. Questa equazione è valida solo in regioni non contenenti correnti. Chari, Campbell, e D’angelo hanno ricavato la formulazione dell’energia dentro il magnete permanente [5]:

Il secondo integrale può essere localizzato solo nei materiali costituiti da magneti permanenti.

Utilizzando l’espansione

Si ottiene

Il secondo termine può essere riscritto utilizzando l’identità di Green

dove: è il dominio contenente l’intera regione; T è la superficie esterna di ; γ è la superficie del magnete ed M0 la magnetizzazione intrinseca permanente di valore costante nella direzione anisotropa. La regione 3D è discretizzata da elementi tetraedrici.

Per una superficie dalla quale non escono le linee di flusso vale:

Il valore del potenziale scalare si calcola minimizzando il funzionale definito nella (7-8):

Dentro ogni elemento la funzione potenziale è calcolata sui quattro vertici tramite una formulazione del primo ordine. Con una approssimazione lineare, il potenziale scalare può essere espresso in ogni punto all’interno del tetraedro attraverso una interpolazione lineare:

(

I coefficienti a, b, c, d in possono essere calcolati da quattro equazioni indipendenti in ognuna delle quali viene fissato il potenziale P1, P2, P3, P4 di uno dei quattro nodi sui vertici.

Sostituendo ognuno dei quattro potenziali ed i valori delle quattro coordinate cartesiane xi, yi, zi . Dopo aver effettuato queste quattro equazioni il potenziale in un punto generico x, y, z risulta:

In pratica il potenziale viene espresso in funzione della somma delle quattro funzioni di forma sui potenziali nodali:

dove è la funzione di forma i-esima. Si ottiene

Il gradiente del potenziale all’interno di ogni elemento può essere ricavato come:

dove

Discretizzando la derivata in (7-11) attraverso l’applicazione delle funzioni di forma si ottiene:

Sia per aria e per ferro invece, la formulazione dell’energia può essere calcolata facilmente:

!     Last change:  PS   17 Apr 2003    5:48 pm
 
Autori: 
Paolo Sordi - Ordine degli ingegneri di Roma N° 22979 - Sezione A
Leonardo Santini - Ordine degli ingegneri di Roma N° 22757 - Sezione A
 
!*************************************************************************
!*************************************************************************
 
 
SUBROUTINE AZZERA_LA_MATRICE_GAUSSJ ()
USE CONFIG_FEM
USE CONFIG_MESH 
IMPLICIT NONE
INTEGER i,j
FUNZIONE_SCALARE = 0.0
VETTORE_PRODOTTO = 0.0
DO i = 1, NNOD
    DO j = 1,NNOD
        MATRICE_GLOBALE_S (i,j) = 0.0
    END DO
END DO
END SUBROUTINE
 
 
 
!*************************************************************************
!*************************************************************************
 
 
SUBROUTINE IMPOSTA_CONDIZIONI_INIZIALI_NEL_SISTEMA_LINEARE_GAUSSJ ()
USE WINTERACTER
USE CONFIG_FEM
USE CONFIG_MESH 
IMPLICIT NONE
INTEGER :: k
INTEGER :: i
DO k = 1 , NNOD
   IF (CONDIZIONE_INIZIALE(k).NE.-1.0) THEN
       DO i=1,NNOD
           MATRICE_GLOBALE_S (k,i) = 0.0
       END DO
       MATRICE_GLOBALE_S (k,k) = 1.0
       VETTORE_PRODOTTO (k) = CONDIZIONE_INIZIALE (k)
       WRITE (1000,*) 'CONDIZIONE_INIZIALE (k)', CONDIZIONE_INIZIALE (k)
   END IF
END DO
PAUSE
END SUBROUTINE
 
 
 
!*************************************************************************
!*************************************************************************
 
 
 
SUBROUTINE CREAZIONE_MATRICE_S_PER_MATERIALI_LINEARI_gaussj ()
USE CONFIG_MESH
USE CONFIG_FEM
USE WINTERACTER
IMPLICIT NONE
DOUBLE PRECISION,DIMENSION (3)   :: grad1,grad2,grad3,grad4
DOUBLE PRECISION,DIMENSION (4,4) :: Matrix_locale_S
DOUBLE PRECISION                 :: dot
DOUBLE PRECISION                 :: value
DOUBLE PRECISION                 :: CALCOLO_VOLUME_TETRAEDRO
DOUBLE PRECISION                 :: permeabilita_relativa
real, DIMENSION (4,4)            :: matrix_ABCD
INTEGER i,k,k1
INTEGER irow,icol
 
DO k= 1,NTETRA
    IF (MATERIALE_TETRAEDRO (k).eq.1.or.MATERIALE_TETRAEDRO (k).eq.2) THEN
        CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD)
        DO i = 1,3
            grad1 (i) = matrix_ABCD (i+1,1)
            grad2 (i) = matrix_ABCD (i+1,2)
            grad3 (i) = matrix_ABCD (i+1,3)
            grad4 (i) = matrix_ABCD (i+1,4)
        END DO
        Matrix_locale_S = 0.0
        Matrix_locale_S (1,1) = DOT (grad1,grad1)
        Matrix_locale_S (2,2) = DOT (grad2,grad2)
        Matrix_locale_S (3,3) = DOT (grad3,grad3)
        Matrix_locale_S (4,4) = DOT (grad4,grad4)
        Matrix_locale_S (1,2) = DOT (grad1,grad2)
        Matrix_locale_S (1,3) = DOT (grad1,grad3)
        Matrix_locale_S (1,4) = DOT (grad1,grad4)
        Matrix_locale_S (2,3) = DOT (grad2,grad3)
        Matrix_locale_S (2,4) = DOT (grad2,grad4)
        Matrix_locale_S (3,4) = DOT (grad3,grad4)
!       CALL CONTROLLA_CHE_LA_MATRICE_SIA_SINGOLARE (Matrix_locale_S)
!        Matrix_locale_S = Matrix_locale_S  / (36.0 * CALCOLO_VOLUME_TETRAEDRO(k))
        Matrix_locale_S = Matrix_locale_S * CALCOLO_VOLUME_TETRAEDRO(k)
        IF (MATERIALE_TETRAEDRO (k).eq.1) THEN
            permeabilita_relativa = 1.0
            Matrix_locale_S = Matrix_locale_S * (2.  * permeabilita_relativa)
        END IF
        IF (MATERIALE_TETRAEDRO (k).eq.2) THEN
            permeabilita_relativa = 100
            Matrix_locale_S = Matrix_locale_S * (2.  * permeabilita_relativa)
        END IF
        DO k1= 1,4
            MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) = MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) + Matrix_locale_S (k1,k1)
        END DO
        MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) + Matrix_locale_S (1,2)
        MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) + Matrix_locale_S (1,3)
        MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) + Matrix_locale_S (1,4)
        MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) + Matrix_locale_S (2,3)
        MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) + Matrix_locale_S (2,4)
        MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) + Matrix_locale_S (3,4)
 
        MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) + Matrix_locale_S (1,2)
        MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) + Matrix_locale_S (1,3)
        MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) + Matrix_locale_S (1,4)
        MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) + Matrix_locale_S (2,3)
        MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) + Matrix_locale_S (2,4)
        MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) + Matrix_locale_S (3,4)
   END IF
END DO
CALL WMESSAGEBOX (0,0,1,'Variabili azzerate. Fine processo di immissione della matrice','')
END SUBROUTINE
 
 
 
!*************************************************************************
!*************************************************************************
 
 
 
SUBROUTINE CREAZIONE_MATRICE_S_E_VETTORE_PER_MAGNETE_PERMANENTE_GAUSSJ ()
USE CONFIG_MESH
USE CONFIG_FEM
USE WINTERACTER
IMPLICIT NONE
DOUBLE PRECISION,DIMENSION (3)   :: grad1,grad2,grad3,grad4
DOUBLE PRECISION,DIMENSION (4,4) :: Matrix_locale_S
DOUBLE PRECISION                 :: dot
DOUBLE PRECISION                 :: value
DOUBLE PRECISION :: CALCOLO_VOLUME_TETRAEDRO
DOUBLE PRECISION :: Campo_coercitivo_Hc
DOUBLE PRECISION :: Br_componente_x
DOUBLE PRECISION :: Br_componente_y
DOUBLE PRECISION :: Br_componente_z
DOUBLE PRECISION :: Br_induzione_residua
DOUBLE PRECISION :: componente_vettore
real, DIMENSION (4,4) :: matrix_ABCD
INTEGER i,k,k1
INTEGER irow,icol
! CALCOLO DEGLI ELEMENTI DELLA MATRICE APPARTENENTI AL MAGNETE
OPEN  (4000,FILE= "componente magnete matrice_superiore.txt")
 
Campo_coercitivo_Hc  = 800000. ! Ampere/m
Br_componente_x = 1.2
Br_componente_y = 0.0
Br_componente_z = 0.0
Br_induzione_residua = DSQRT (Br_componente_x ** 2.0 + Br_componente_y ** 2.0 + Br_componente_z ** 2.0)
DO k = 1, NTETRA
   IF (MATERIALE_TETRAEDRO (k).EQ.3) THEN
       CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD)
       DO i = 1,3
           grad1 (i) = matrix_ABCD (i+1,1)
           grad2 (i) = matrix_ABCD (i+1,2)
           grad3 (i) = matrix_ABCD (i+1,3)
           grad4 (i) = matrix_ABCD (i+1,4)
       END DO
       Matrix_locale_S = 0.0
       Matrix_locale_S (1,1) =  DOT(grad1,grad1)
       Matrix_locale_S (2,2) =  DOT(grad2,grad2)
       Matrix_locale_S (3,3) =  DOT(grad3,grad3)
       Matrix_locale_S (4,4) =  DOT(grad4,grad4)
       Matrix_locale_S (1,2) =  DOT(grad1,grad2)
       Matrix_locale_S (1,3) =  DOT(grad1,grad3)
       Matrix_locale_S (1,4) =  DOT(grad1,grad4)
       Matrix_locale_S (2,3) =  DOT(grad2,grad3)
       Matrix_locale_S (2,4) =  DOT(grad2,grad4)
       Matrix_locale_S (3,4) =  DOT(grad3,grad4)
!       CALL CONTROLLA_CHE_LA_MATRICE_SIA_SINGOLARE (Matrix_locale_S)
       Matrix_locale_S = Matrix_locale_S * (Campo_coercitivo_Hc / Br_induzione_residua)
!       Matrix_locale_S = Matrix_locale_S / (36.0 * CALCOLO_VOLUME_TETRAEDRO(K))
       Matrix_locale_S = Matrix_locale_S * CALCOLO_VOLUME_TETRAEDRO(K)
       Matrix_locale_S = Matrix_locale_S / 2.0
       DO k1= 1,4
            MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) = MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) + Matrix_locale_S (k1,k1)
       END DO
       MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) + Matrix_locale_S (1,2)
       MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) + Matrix_locale_S (1,3)
       MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) + Matrix_locale_S (1,4)
       MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) + Matrix_locale_S (2,3)
       MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) + Matrix_locale_S (2,4)
       MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) + Matrix_locale_S (3,4)
 
       MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) + Matrix_locale_S (1,2)
       MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) + Matrix_locale_S (1,3)
       MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) + Matrix_locale_S (1,4)
       MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) + Matrix_locale_S (2,3)
       MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) + Matrix_locale_S (2,4)
       MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) + Matrix_locale_S (3,4)
   END IF
END DO
CALL WMESSAGEBOX (0,0,1,'Fine del processo di immissione nella matrice S ','ciao')
 
DO k = 1 , NTETRA
   IF (MATERIALE_TETRAEDRO (k).EQ.3) THEN
       CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD)
       DO i=1,4
             componente_vettore = Br_componente_x * matrix_ABCD (2,i)  &amp;
                                + Br_componente_y * matrix_ABCD (3,i)  &amp;
                                + Br_componente_z * matrix_ABCD (4,i)
             componente_vettore = ( Campo_coercitivo_Hc / Br_induzione_residua ) * componente_vettore
!            componente_vettore = componente_vettore / 2.0
             componente_vettore = componente_vettore * CALCOLO_VOLUME_TETRAEDRO (k)
             VETTORE_PRODOTTO (NT(k,i)) = VETTORE_PRODOTTO (NT(k,i)) + componente_vettore
       END DO
   END IF
END DO
CALL WMESSAGEBOX (0,0,1,'Fine del processo di immissione nel vettore forzamento','')
END SUBROUTINE
 
 
!*************************************************************************
!*************************************************************************
 
 
SUBROUTINE SOLUZIONE_ELEMENTI_FINITI_CON_GAUSSJ
USE CONFIG_FEM
USE CONFIG_MESH
REAL ,DIMENSION (MAXNODI) :: VETT_PRODOTTO
WRITE (1000,*) "MATRICE_GLOBALE_S"
DO i = 1, NNOD
    DO j = 1,NNOD
        IF (MATRICE_GLOBALE_S (i,j).ne.0.0) WRITE (1000,*) i,j, MATRICE_GLOBALE_S (i,j)
    END DO
END DO
WRITE (1000,*)  'VETT_PRODOTTO'
VETT_PRODOTTO = REAL (VETTORE_PRODOTTO)
DO j = 1,NNOD
    WRITE (1000,*) j, VETT_PRODOTTO (j)
END DO
CALL GAUSSJ (MATRICE_GLOBALE_S,NNOD,MAXNODI,VETT_PRODOTTO,1,1)
FUNZIONE_SCALARE = VETTORE_PRODOTTO
PAUSE 
END SUBROUTINE

! Last change: PS 17 Apr 2003 5:48 pm Autori: Paolo Sordi - Ordine degli ingegneri di Roma N° 22979 - Sezione A Leonardo Santini - Ordine degli ingegneri di Roma N° 22757 - Sezione A !************************************************************************* !************************************************************************* SUBROUTINE AZZERA_LA_MATRICE_GAUSSJ () USE CONFIG_FEM USE CONFIG_MESH IMPLICIT NONE INTEGER i,j FUNZIONE_SCALARE = 0.0 VETTORE_PRODOTTO = 0.0 DO i = 1, NNOD DO j = 1,NNOD MATRICE_GLOBALE_S (i,j) = 0.0 END DO END DO END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE IMPOSTA_CONDIZIONI_INIZIALI_NEL_SISTEMA_LINEARE_GAUSSJ () USE WINTERACTER USE CONFIG_FEM USE CONFIG_MESH IMPLICIT NONE INTEGER :: k INTEGER :: i DO k = 1 , NNOD IF (CONDIZIONE_INIZIALE(k).NE.-1.0) THEN DO i=1,NNOD MATRICE_GLOBALE_S (k,i) = 0.0 END DO MATRICE_GLOBALE_S (k,k) = 1.0 VETTORE_PRODOTTO (k) = CONDIZIONE_INIZIALE (k) WRITE (1000,*) 'CONDIZIONE_INIZIALE (k)', CONDIZIONE_INIZIALE (k) END IF END DO PAUSE END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE CREAZIONE_MATRICE_S_PER_MATERIALI_LINEARI_gaussj () USE CONFIG_MESH USE CONFIG_FEM USE WINTERACTER IMPLICIT NONE DOUBLE PRECISION,DIMENSION (3) :: grad1,grad2,grad3,grad4 DOUBLE PRECISION,DIMENSION (4,4) :: Matrix_locale_S DOUBLE PRECISION :: dot DOUBLE PRECISION :: value DOUBLE PRECISION :: CALCOLO_VOLUME_TETRAEDRO DOUBLE PRECISION :: permeabilita_relativa real, DIMENSION (4,4) :: matrix_ABCD INTEGER i,k,k1 INTEGER irow,icol DO k= 1,NTETRA IF (MATERIALE_TETRAEDRO (k).eq.1.or.MATERIALE_TETRAEDRO (k).eq.2) THEN CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD) DO i = 1,3 grad1 (i) = matrix_ABCD (i+1,1) grad2 (i) = matrix_ABCD (i+1,2) grad3 (i) = matrix_ABCD (i+1,3) grad4 (i) = matrix_ABCD (i+1,4) END DO Matrix_locale_S = 0.0 Matrix_locale_S (1,1) = DOT (grad1,grad1) Matrix_locale_S (2,2) = DOT (grad2,grad2) Matrix_locale_S (3,3) = DOT (grad3,grad3) Matrix_locale_S (4,4) = DOT (grad4,grad4) Matrix_locale_S (1,2) = DOT (grad1,grad2) Matrix_locale_S (1,3) = DOT (grad1,grad3) Matrix_locale_S (1,4) = DOT (grad1,grad4) Matrix_locale_S (2,3) = DOT (grad2,grad3) Matrix_locale_S (2,4) = DOT (grad2,grad4) Matrix_locale_S (3,4) = DOT (grad3,grad4) ! CALL CONTROLLA_CHE_LA_MATRICE_SIA_SINGOLARE (Matrix_locale_S) ! Matrix_locale_S = Matrix_locale_S / (36.0 * CALCOLO_VOLUME_TETRAEDRO(k)) Matrix_locale_S = Matrix_locale_S * CALCOLO_VOLUME_TETRAEDRO(k) IF (MATERIALE_TETRAEDRO (k).eq.1) THEN permeabilita_relativa = 1.0 Matrix_locale_S = Matrix_locale_S * (2. * permeabilita_relativa) END IF IF (MATERIALE_TETRAEDRO (k).eq.2) THEN permeabilita_relativa = 100 Matrix_locale_S = Matrix_locale_S * (2. * permeabilita_relativa) END IF DO k1= 1,4 MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) = MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) + Matrix_locale_S (k1,k1) END DO MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) + Matrix_locale_S (1,2) MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) + Matrix_locale_S (1,3) MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) + Matrix_locale_S (1,4) MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) + Matrix_locale_S (2,3) MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) + Matrix_locale_S (2,4) MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) + Matrix_locale_S (3,4) MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) + Matrix_locale_S (1,2) MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) + Matrix_locale_S (1,3) MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) + Matrix_locale_S (1,4) MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) + Matrix_locale_S (2,3) MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) + Matrix_locale_S (2,4) MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) + Matrix_locale_S (3,4) END IF END DO CALL WMESSAGEBOX (0,0,1,'Variabili azzerate. Fine processo di immissione della matrice','') END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE CREAZIONE_MATRICE_S_E_VETTORE_PER_MAGNETE_PERMANENTE_GAUSSJ () USE CONFIG_MESH USE CONFIG_FEM USE WINTERACTER IMPLICIT NONE DOUBLE PRECISION,DIMENSION (3) :: grad1,grad2,grad3,grad4 DOUBLE PRECISION,DIMENSION (4,4) :: Matrix_locale_S DOUBLE PRECISION :: dot DOUBLE PRECISION :: value DOUBLE PRECISION :: CALCOLO_VOLUME_TETRAEDRO DOUBLE PRECISION :: Campo_coercitivo_Hc DOUBLE PRECISION :: Br_componente_x DOUBLE PRECISION :: Br_componente_y DOUBLE PRECISION :: Br_componente_z DOUBLE PRECISION :: Br_induzione_residua DOUBLE PRECISION :: componente_vettore real, DIMENSION (4,4) :: matrix_ABCD INTEGER i,k,k1 INTEGER irow,icol ! CALCOLO DEGLI ELEMENTI DELLA MATRICE APPARTENENTI AL MAGNETE OPEN (4000,FILE= "componente magnete matrice_superiore.txt") Campo_coercitivo_Hc = 800000. ! Ampere/m Br_componente_x = 1.2 Br_componente_y = 0.0 Br_componente_z = 0.0 Br_induzione_residua = DSQRT (Br_componente_x ** 2.0 + Br_componente_y ** 2.0 + Br_componente_z ** 2.0) DO k = 1, NTETRA IF (MATERIALE_TETRAEDRO (k).EQ.3) THEN CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD) DO i = 1,3 grad1 (i) = matrix_ABCD (i+1,1) grad2 (i) = matrix_ABCD (i+1,2) grad3 (i) = matrix_ABCD (i+1,3) grad4 (i) = matrix_ABCD (i+1,4) END DO Matrix_locale_S = 0.0 Matrix_locale_S (1,1) = DOT(grad1,grad1) Matrix_locale_S (2,2) = DOT(grad2,grad2) Matrix_locale_S (3,3) = DOT(grad3,grad3) Matrix_locale_S (4,4) = DOT(grad4,grad4) Matrix_locale_S (1,2) = DOT(grad1,grad2) Matrix_locale_S (1,3) = DOT(grad1,grad3) Matrix_locale_S (1,4) = DOT(grad1,grad4) Matrix_locale_S (2,3) = DOT(grad2,grad3) Matrix_locale_S (2,4) = DOT(grad2,grad4) Matrix_locale_S (3,4) = DOT(grad3,grad4) ! CALL CONTROLLA_CHE_LA_MATRICE_SIA_SINGOLARE (Matrix_locale_S) Matrix_locale_S = Matrix_locale_S * (Campo_coercitivo_Hc / Br_induzione_residua) ! Matrix_locale_S = Matrix_locale_S / (36.0 * CALCOLO_VOLUME_TETRAEDRO(K)) Matrix_locale_S = Matrix_locale_S * CALCOLO_VOLUME_TETRAEDRO(K) Matrix_locale_S = Matrix_locale_S / 2.0 DO k1= 1,4 MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) = MATRICE_GLOBALE_S (NT(k,k1),NT(k,k1)) + Matrix_locale_S (k1,k1) END DO MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,2)) + Matrix_locale_S (1,2) MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,3)) + Matrix_locale_S (1,3) MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,1),NT(k,4)) + Matrix_locale_S (1,4) MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,3)) + Matrix_locale_S (2,3) MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,4)) + Matrix_locale_S (2,4) MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,4)) + Matrix_locale_S (3,4) MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,2),NT(k,1)) + Matrix_locale_S (1,2) MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,1)) + Matrix_locale_S (1,3) MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,1)) + Matrix_locale_S (1,4) MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,3),NT(k,2)) + Matrix_locale_S (2,3) MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,2)) + Matrix_locale_S (2,4) MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) = MATRICE_GLOBALE_S (NT(k,4),NT(k,3)) + Matrix_locale_S (3,4) END IF END DO CALL WMESSAGEBOX (0,0,1,'Fine del processo di immissione nella matrice S ','ciao') DO k = 1 , NTETRA IF (MATERIALE_TETRAEDRO (k).EQ.3) THEN CALL CALCOLA_COEFFICIENTI_A_B_C_D (k, matrix_ABCD) DO i=1,4 componente_vettore = Br_componente_x * matrix_ABCD (2,i) & + Br_componente_y * matrix_ABCD (3,i) & + Br_componente_z * matrix_ABCD (4,i) componente_vettore = ( Campo_coercitivo_Hc / Br_induzione_residua ) * componente_vettore ! componente_vettore = componente_vettore / 2.0 componente_vettore = componente_vettore * CALCOLO_VOLUME_TETRAEDRO (k) VETTORE_PRODOTTO (NT(k,i)) = VETTORE_PRODOTTO (NT(k,i)) + componente_vettore END DO END IF END DO CALL WMESSAGEBOX (0,0,1,'Fine del processo di immissione nel vettore forzamento','') END SUBROUTINE !************************************************************************* !************************************************************************* SUBROUTINE SOLUZIONE_ELEMENTI_FINITI_CON_GAUSSJ USE CONFIG_FEM USE CONFIG_MESH REAL ,DIMENSION (MAXNODI) :: VETT_PRODOTTO WRITE (1000,*) "MATRICE_GLOBALE_S" DO i = 1, NNOD DO j = 1,NNOD IF (MATRICE_GLOBALE_S (i,j).ne.0.0) WRITE (1000,*) i,j, MATRICE_GLOBALE_S (i,j) END DO END DO WRITE (1000,*) 'VETT_PRODOTTO' VETT_PRODOTTO = REAL (VETTORE_PRODOTTO) DO j = 1,NNOD WRITE (1000,*) j, VETT_PRODOTTO (j) END DO CALL GAUSSJ (MATRICE_GLOBALE_S,NNOD,MAXNODI,VETT_PRODOTTO,1,1) FUNZIONE_SCALARE = VETTORE_PRODOTTO PAUSE END SUBROUTINE

La soluzione di campo 3D appena descritta è stata applicata alla macchina AFPM. La geometria scelta prende un polo elettrico di macchina. Le dimensioni principali della macchina solo riportate nella Tabella 7-1.

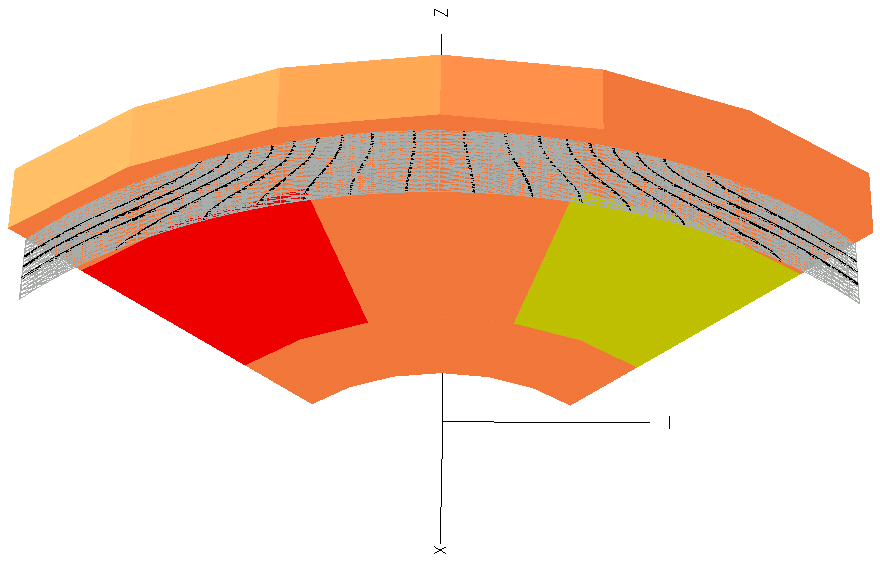
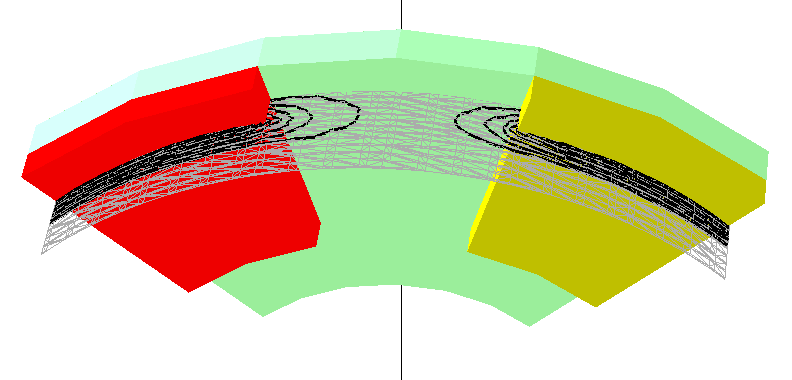
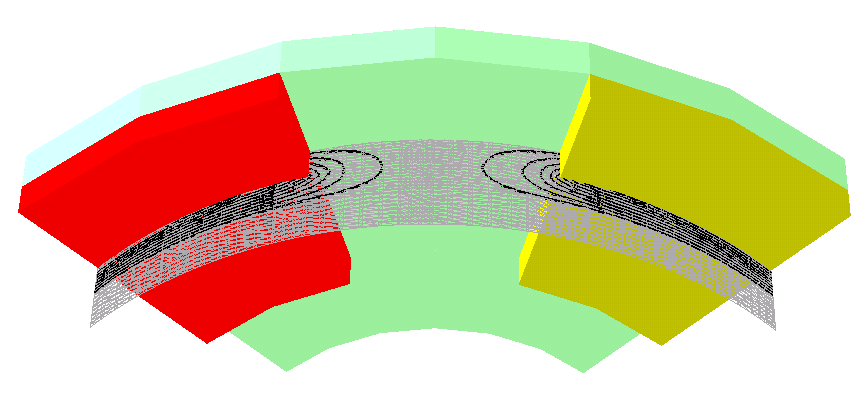
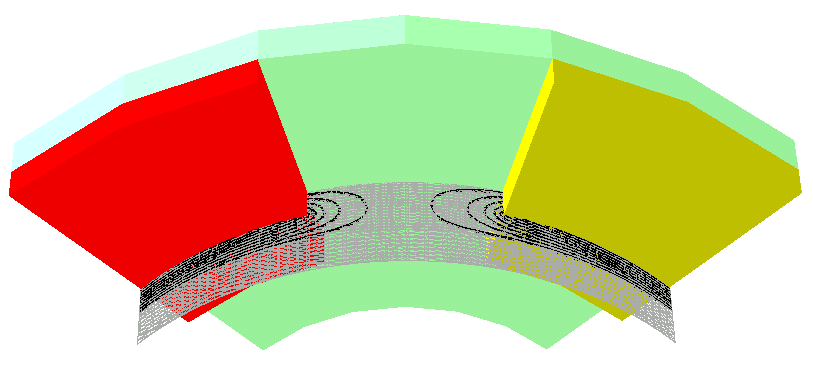
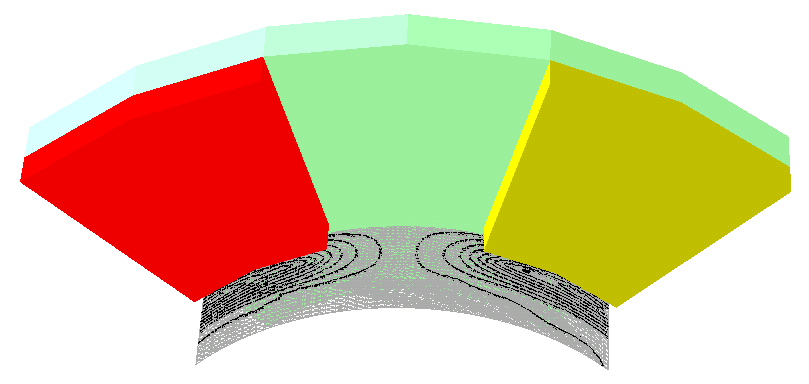
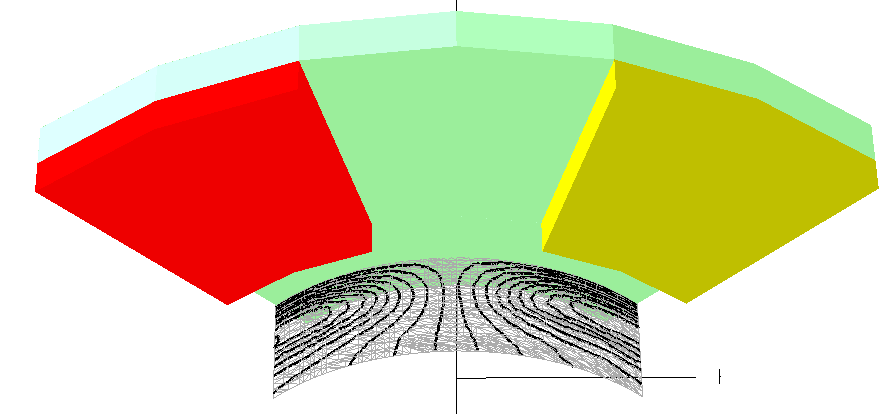
Dalla Figura 7-3 alla 7-8 vengono mostrate le linee equipotenziali calcolate su una serie di sezioni cilindriche effettuate sulla macchina.

Tabella 71 Dimensioni della macchina simulata

Ro raggio esterno di macchina	80 mm
Ri raggio interno di macchina	45 mm
τp passo polare	90°
τm passo del magnete	54 deg
Azr spessore asssiale del disco rotorico	10 mm
Azm Spessore assiale del PM	10 mm
Aztr Spessore assiale totale del disco rotorico	19 mm

Il materiale per i magneti permanenti usato nella simulazione presenta la più alta magnetizzazione residua, vale a dire i magneti a terre rare (NdFeB). La caratteristica del magnete scelto sono il campo coercitivo Hc=1000 kA/m; l’induzione magnetica residua Br=1.2 T. L’analisi del MSP e conseguentemente dell’induzione magnetica B è necessaria per determinare la coppia di macchina. Dato che il potenziale MSP è definito dal campo magnetico $\overrightarrow{H}$ , le linee equipotenziali giacciono prevalentemente dentro il traferro ed il magnete permanente della macchina. Per calcolare il flusso concatenato in fase di post-processing deve essere sottolineato che comunque la soluzione di campo del MSP è presente anche all’interno del ferro di statore nonostante sia di valore più piccolo.

Figura – Vista delle linee equipotenziali sul raggio esterno di macchina.

Figura – Vista delle linee equipotenziali su una sezione radiale di raggio R=71.25 mm.

Figura – Vista delle linee equipotenziali su una sezione radiale di raggio (R=62.5 mm)

Figura – Vista delle linee equipotenziali su una sezione radiale di raggio (R=53.75 mm).

Figura 77 Vista delle linee equipotenziali su una sezione radiale corrispondente al raggio interno

Figura – Vista delle linee equipotenziali su una sezione radiale di raggio minore (R=35 mm)

BIBLIOGRAFIA

Campbell, P.; Chari, M.; D’Angelo, J. – Three-dimensional finite element solution of permanent magnet machines – Magnetics, IEEE Transactions on ,Volume: 17 , Issue: 6 , Nov 1981 Pages:2997 – 2999.
Rosu, M.; Arkkio, A.; Jokinen, T.; Mantere, J.; Westerlund, J. – Demagnetisation state of permanent magnets in large output power permanent magnet synchronous motor – Electric Machines and Drives, 1999. International Conference IEMD ’99 , 9-12 May 1999 Pages:776 – 778.
Adnanes, A.K. – Torque analysis of permanent magnet synchronous motors – Power Electronics Specialists Conference, 1991. PESC ’91 Record., 22nd Annual IEEE , 24-27 June 1991 Pages:695 – 701.
Chan, T.F.; Lie-Tong Yan – Analysis and performance of a surface-mounted NdFeB permanent-magnet AC generator – Advances in Power System Control, Operation and Management, 1997. APSCOM-97. Fourth International Conference on (Conf. Publ. No. 450) , Volume: 2 , 11-14 Nov. 1997 Pages:718 – 722 vol.2.
P. Campbell, M.V.K. Chari, J. D’Angelo – Three dimensional finite element solution of permanent magnet machines – IEEE transactions on magnetics, Vol. 17, N° 6, November 1981.
Sitapati, K.; Krishnan, R. – Performance comparisons of radial and axial field, permanent-magnet, brushless machines – Industry Applications, IEEE Transactions on , Volume: 37 , Issue: 5 , Sept.-Oct. 2001 Pages:1219 – 1226.
Campbell, P.; Nafisi, A. – The effect of iron powders on the utilization of permanent magnet materials in advanced motors – Magnetics, IEEE Transactions on ,Volume: 16 , Issue: 5 , Sep 1980 Pages:690 – 692.
F. Piriou, A. Razek – Calculation of saturated inductances for numerical simulation of synchronous machines – IEEE-Mag.19, n6, pp 2628-2631, nov 83.
Hanson, A.J.; Heng, P.A. – Four-dimensional views of 3D scalar fields – Visualization, 1992. Proceedings., IEEE Conference on , 19-23 Oct. 1992 Pages:84 – 91.
Mayergoyz, I.; Chari, M.; D’Angelo, J. – A new scalar potential formulation for three-dimensional magnetostatic problems – Magnetics, IEEE Transactions on , Volume: 23 , Issue: 6 , Nov 1987 Pages:3889 – 3894.
Seong-Pyo Hong; Han-Sam Cho; Hae-Seok Lee; Hyun-Rae Cho; Hak-Yong Lee – Effect of the magnetization direction in permanent magnet on motor characteristics – Magnetics, IEEE Transactions on , Volume: 35 , Issue: 3 , May 1999 Pages:1231 – 1234.
Ooshima, M.; Chiba, A.; Fukao, T.; Rahman, M.A. – Design and analysis of permanent magnet-type bearingless motors – Industrial Electronics, IEEE Transactions on , Volume: 43 , Issue: 2 , April 1996 Pages:292 – 299.
Wang Ke-Qin; Jiang Zhong-Wei; Sun Yu-Shi – 3D finite element solution of complex magnetostatic problem involving axial and radial excitation-using a single scalar potential – Magnetics, IEEE Transactions on , Volume: 26 , Issue: 2 , Mar 1990 Pages:356 – 359.
Parviainen, A.; Niemela, M.; Pyrhonen, J. – Modelling of axial flux PM machines – Electric Machines and Drives Conference, 2003. IEMDC’03. IEEE International , Volume: 3 , 1-4 June 2003 Pages:1955 – 1961 vol.3.
Aydin, M.; Huang, S.; Lipo, T.A. – Optimum design and 3D finite element analysis of nonslotted and slotted internal rotor type axial flux PM disc machines – Power Engineering Society Summer Meeting, 2001. IEEE , Volume: 3 , 15-19 July 2001 Pages:1409 – 1416 vol.3.

Consulenza Tecnica

Analisi FE | Modellazione Magneti Permanenti

PROGETTO DI MACCHINE SINCRONE A FLUSSO ASSIALE A MAGNETI PERMANENTI. ANALISI 3D AGLI ELEMENTI FINITI. POTENZIALE SCALARE

SOLUZIONE AGLI ELEMENTI FINITI IN CONDIZIONI DI FUNZIONAMENTO A VUOTO DELLA MACCHINA (CORRENTE NULLA)

Lascia un commento Annulla risposta