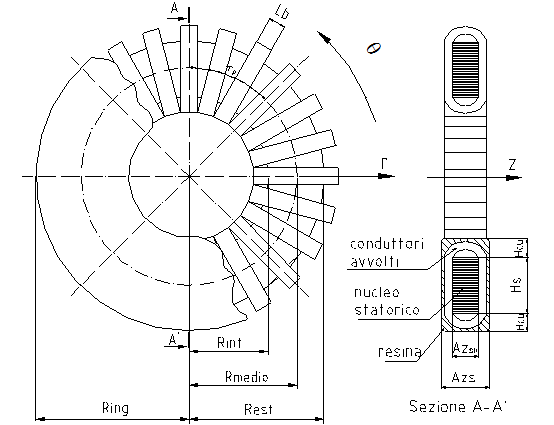
STUDIO DEL CAMPO MAGNETICO AL TRAFERRO CON UN PROGRAMMA AGLI ELEMENTI FINITI
Fino a questo punto, il calcolo delle grandezze fondamentali della macchina a disco può esere effettuato formulando l’ipotesi di flusso disperso nullo e linee del campo magnetico al traferro esattamente parallele all’asse azimutale. Con queste ipotesi, il campo magnetico al traferro assume l’andamento di un’onda rettangolare (Figura 1-10b). Una volta effettuate queste assunzioni, si è ricavata una forma d’onda rettangolare della fem indotta su di una spira di spessore infinitesimo (Figura 1-10d).
I risultati ottenuti nei capitoli precedenti sono in ogni modo confrontabili con le misure effettuate. Tuttavia quasi tutte le ottimizzazioni svolte nel Capitolo quattro hanno messo in evidenza dei limiti notevoli nelle considerazioni progettuali effettuate.
Osservando i risultati del Capitolo quattro si evince che la maggior parte dei progetti finali forniscono una macchina con spessore del rame Azcu pari a 7.5mm, questo valore è stato imposto necessariamente come vincolo strutturale perché il modello non tiene conto dell’aumento del flusso disperso all’aumentare dello spessore della bobina.
Nella Tabella 5-1 sono riportate le soluzioni finali di due ottimizzazioni che presentano specifiche identiche a quelle del Paragrafo 4.3. La prima soluzione proposta è uguale a quella della Tabella 4-1. La seconda soluzione è stata invece ricavata senza fissare alcuna condizione sullo spessore massimo della bobina.
Tabella 5-1 Esempio di variazione della soluzione in assenza di vincoli restrittivi
|
Rest |
Kr |
Poli |
Kpest |
Kpint |
Azcu |
Cm (P) |
m |
Peso |
Perdite |
Jmax |
|
Soluzione con vincolo su Azcu |
||||||||||
|
226 |
0.5 |
24 |
0.85 |
0.85 |
7.5 |
367 |
92.5 |
55.8 |
627 |
4.35 |
|
Soluzione senza vincoli su Azcu |
||||||||||
|
193 |
0.519 |
24 |
0.85 |
0.85 |
40 |
485.8 |
95.98 |
103.0 |
426 |
1.99 |
Dalla seconda soluzione della Tabella si rileva che il sistema di ottimizzazione, lasciato libero di variare lo spessore del rame, lo aumenta fino a 40 mm innalzando la coppia nominale di 118 Nm. Un tale risultato, viste le condizioni imposte, non deve stupire perché il modello di progettazione considera il flusso magnetico costante e perpendicolare in tutto il traferro. Nel caso in cui il flusso disperso dai magneti fosse veramente nullo, la soluzione potrebbe anche essere adottabile (tra l’altro, si guadagna il 3% sul rendimento). In realtà, la macchina costruita con i dati della 2° soluzione fornirebbe prestazioni ben al di sotto di quelle previste. Questa discordanza sui dati reali, può essere implicata all’aver trascurato la quota parte del flusso magnetico che non si concatena con le spire di macchina oppure che si concatena solo parzialmente.
Un altro vincolo strutturale adottato è stato quello sulla superficie rotorica massima che i magneti possono occupare (si è imposto: Kp<0.85 sul raggio interno ed esterno). Facendo sempre il confronto con la soluzione della Tabella 4-1, si vuole osservare quali sono le variazioni della convergenza se il sistema è lasciato libero di variare la forma dei magneti su tutto il passo polare disponibile. Nella Tabella 5-2 sono riportati i risultati finali nello studio di questa problematica.
Tabella 5-2 Esempio di variazione della soluzione in assenza di vincoli restrittivi
|
Rest |
Kr |
Poli |
Kpest |
Kpint |
Azcu |
Cm (P) |
m |
Peso |
Perdite |
Jmax |
|
226 |
0.49 |
26 |
0.97 |
0.97 |
7.5 |
374 |
92.5 |
59.9 |
631 |
4.32 |
Si può rilevare che nel progetto finale i magneti tendono ad occupare quasi tutta la superficie rotorica disponibile. Anche in questo caso i dati sulle prestazioni della macchina sono molto ottimistici sia perché non si tiene conto dell’aumento del flusso disperso all’aumentare del coefficiente Kp, sia perché le condizioni di smaltimento termico del calore tendono a peggiorare quando diminuisce il volume di aria tra due magneti adiacenti. Uno degli scopi di questo Capitolo consiste nel correggere i risultati ottenuti analizzando accuratamente la conformazione del campo magnetico al traferro con un programma agli elementi finiti. L’idea è quella di correggere la forma d’onda della fem indotta nelle bobine.
Gli obiettivi pratici di questo affinamento sono i seguenti:
-
Raggiungere una maggiore precisione nel calcolo delle grandezze di interesse.
-
Effettuare le ottimizzazione della macchina a disco senza dover imporre i vincoli del Paragrafo 4.1.
-
Procedere all’introduzione della coppia pulsante della macchina come funzione di prestazione da includere nei problemi di ottimizzazione.
IMPOSTAZIONE DEL PROBLEMA
Nella Figura 1-8 è riportato lo schema della geometria minima di una macchina a flusso assiale con la relativa soluzione agli elementi finiti. Quando viene eseguito il calcolo della fem la corona rotorica viene divisa in settori (vedere Figura 2-1). La problematica da risolvere consiste nell’effettuare uno studio agli elementi finiti come quello nella Figura 1-8 per ogni singolo settore che viene creato durante l’elaborazione del progetto. Le strade che possono essere seguite sono due:
-
Si potrebbe costruire un algoritmo che conoscendo tutti i dati dimensionali del settore, effettui uno studio agli elementi finiti per ricavare l’andamento del campo al traferro.
-
Si potrebbe ricavare l’andamento del campo al traferro prelevando le soluzioni di interesse in una libreria costruita appositamente. In questo caso, bisognerebbe effettuare un determinato numero di prove su un programma agli elementi finiti, ricavando gli andamenti del campo al traferro per un certo numero di configurazioni. Con questi dati si costruirebbe una libreria da consultare per ogni nuova geometria.
La costruzione di un algoritmo che effettui il calcolo del campo con la teoria degli elementi finiti, non presenta complicazioni elevate perché la geometria da studiare è relativamente semplice. Infatti, il problema della triangolarizzazione deve essere risolto una sola volta perché la topologia dello schema rimane sempre la stessa. Questa strada presenta il vantaggio di fornire la soluzione esatta del campo per ogni settore da studiare.
Il secondo criterio di risoluzione della problematica è meno raffinato del primo però permette di evitare la costruzione di una procedura relativamente complessa. La costruzione di una libreria di soluzioni è un processo molto lento. Tuttavia il vantaggio nel prelevare delle soluzioni già esistenti invece di dover crearne sempre delle nuove è molto elevato. Si deve ricordare, infatti, che per il calcolo di un’unica fem di macchina il sistema esegue la divisione della corona rotorica in una miriade di settori, su ognuno dei quali dovrebbe essere effettuato lo studio agli elementi finiti. Bisogna inoltre considerare che in un processo di ottimizzazione possono essere elaborati migliaia di progetti.
In conclusione, un vantaggio considerevole nella costruzione di una libreria di soluzioni, è sicuramente il risparmio di tempo che si può ottenere durante i processi di progettazione e di ottimizzazione.
ANALISI DELLA GEOMETRIA MINIMA DELLA MACCHINA
Nella Figura 5-1 viene riportato lo schema della geometria minima della macchina a flusso assiale su cui bisogna effettuare lo studio agli elementi finiti.
Figura 5-1 Schema con quote della geometria minima della macchina
Questa geometria viene disegnata per ogni settore i-esimo della Figura 2-1. In generale, tutte le quote dello schema saranno variabili da progetto a progetto. Se non si stabilissero delle relazioni tra le grandezze dimensionali la costruzione di una libreria del campo al traferro dovrebbe prevedere un numero elevato di configurazioni geometriche da studiare. Di seguito vengono effettuate delle considerazioni per stabilire legami dimensionali tra le varie grandezze, in modo da ridurre il campo di rilevazione.
-
Il rapporto Ka=Aza/Azm per le considerazioni del Paragrafo 1.3.4 è praticamente determinato con la Formula 1.3.4-4. Il parametro Ka dovrà essere circa unitario
-
Gli spessori del rotore Azr e dello statore Azsn non influiscono sulla soluzione del campo perché può essere mantenuta l’ipotesi di riluttanza nulla nel ferro.
Dalle considerazioni appena effettuate si evince che l’andamento del campo al traferro in una geometria minima può essere calcolato quando vengono fornite tre sole grandezze: il passo polare τm; il passo del magnete τp; l’altezza del magnete Azm.
C’è inoltre da considerare che le geometrie simili, vale a dire con lo stesso rapporto tra queste tre grandezze forniscono soluzioni del campo al traferro identiche. Per questo motivo le variabili in gioco nello studio dello schema basilare possono essere i due seguenti rapporti:
;
(5.3-1)
Bisogna a questo punto definire quali sono i limiti di variazione di questi due coefficienti. Il rapporto Kp può variare teoricamente tra zero ed uno. In pratica, assumerà sempre valori compresi tra 0.5 ed 1. Siccome il sistema di ottimizzazione deve anche analizzare progetti che andranno scartati si stabilisce che il dominio di Kp varia tra 0.4 ed 1. Il rapporto Kk invece, assume normalmente valori più bassi (Kk= 0.05÷0.3).
Nelle Figure 5-2, 5-3 vengono riportate due soluzioni agli elementi finiti ricavate su due diverse geometrie della macchina. Dalle Figure è possibile rilevare la differenza negli andamenti delle linee equipotenziali.
Nella Figura 5-4 sono riportati i due andamenti del campo di induzione normale al traferro ricavati sulle linee x’-x’’. Con le linee tratteggiate si indica il campo di induzione teorico in assenza di flusso disperso. Il confronto con le curve teoriche mette in risalto l’errore nell’approssimazione adottata: per la seconda configurazione (Figura 5-3, con Kp=1) si può notare il divario tra la soluzione ideale e quella reale.
Figura 5-2 Soluzione del campo per una geometria con Kk=0.15 e Kp=0.5
Figura 5-3 Soluzione del campo per una geometria con Kk=0.15 e Kp=1
Figura 5-4 Grafico del campo al traferro sulle linee x’-x’’
Un fenomeno evidente nello studio delle due curve risulta l’aumento del valore massimo del campo al traferro al crescere del coefficiente Kp.
L’aumento del campo avviene a causa del minore tratto in aria che le linee del campo devono percorrere prima della richiusura. Infatti, se il magnete occupa tutto lo spazio polare, il flusso disperso si richiude in un circuito di riluttanza più piccola.
A questo punto si presenta il problema di determinare quale sia la linea x’-x’’ più adatta per misurare il campo di induzione al traferro. Nella Figura 5-5 è riportato lo studio di una nuova configurazione. Nella zona del traferro sono tracciate 5 segmenti su ognuno dei quali viene rilevato il valore del campo di induzione normale.
Figura 5-5 Linee equipotenziali del campo per una geometria con Kk=0.15 e Kp=0.7
I risultati ottenuti sono riportati nella Figura 5-6. Dall’osservazione delle cinque curve della Figura si evince innanzi tutto, che le soluzioni del campo presentano un errore minore quando i segmenti si avvicinano al ferro di statore. Questo avviene perché la rifinitura della mesh è più accurata nelle zone in cui si addensano le linee del campo.
E’ importante osservare che tranne la prima curva rilevata in prossimità del magnete le altre curve presentano un andamento praticamente identico. Questo vuol dire che le linee del campo che non deviano immediatamente, sono attirate dalla quota parte di circuito di riluttanza trascurabile dello statore.
Lo studio del campo al traferro viene effettuato per calcolare il flusso concatenato con le bobine di macchina. Lo studio della curva n°1 non è quindi rilevante perché deve essere lasciato lo spazio per il tratto in aria (di spessore Azt), e per lo strato di resina (di spessore Azres). In conclusione, il rilievo del campo sarà effettuato su di una linea che dimezza la sezione delle bobine. La linea prescelta avrà quindi una distanza pari ad dalla sezione dello statore.
Figura 5-6 Curve del campo B al traferro, rilevate sulle linee della Figura 5-5
Il dominio della funzione è circoscritto in una superficie disegnata nella Figura 5-7. Questa zona deve essere studiata estesamente in modo da creare un alto numero di configurazioni possibili. Per questo motivo la superficie rettangolare viene ricoperta da una griglia di linee. Nei punti di intersezione delle linee sarà calcolato l’andamento del campo al traferro che verrà memorizzato nella libreria delle soluzioni.
Figura 5-7 Grafico delle possibili configurazioni della geometria minima
Si suppone che la geometria da studiare sia quella identificata nel punto Y. Il calcolo della soluzione avverrà effettuando l’interpolazione delle curve BA(x), BB(x), BC(x), BD(x), rispettivamente delle geometrie A, B, C, D che si trovano intorno alla soluzione cercata. Di seguito vengono descritti i passi necessari per risalire alla curva BY(x):
1) Il primo passo consiste nel prelevare le quattro curve BA(x), BB(x), BC(x), BD(x) dalla libreria costruita. Per ogni angolo elettrico xi desiderato si deve calcolare il valore BY(xi, Kk, Kp).
-
Nel dominio delimitato dal rettangolo di vertici A, B, C, D si costruisce una funzione del tipo:
(5.3-2)
Questa funzione deve essere tale da fornire i valori esatti B(xi), nei punti A, B, C, D. I coefficienti a1, a2, a3 ed a4 sono calcolati proprio secondo questa condizione. Si deve risolvere di conseguenza, il seguente sistema di equazioni:
(5.3-3)
Come si può osservare i parametri a1, a2, a3 ed a4 variano con l’angolo elettrico xi. Questo vuol dire che per ricavare una curva del campo al traferro per N punti, è necessario ricavare N volte i quattro coefficienti. Il peso computazionale di questo procedimento non è comunque elevato perché l’inversione della matrice di dimensioni quattro per quattro della (5.3-3) avviene una sola volta per ogni interpolazione rettangolare.
Una volta ricavati i quattro coefficienti della funzione è possibile sfruttare la relazione 5.3-2 per risalire a tutti i valori del campo al traferro desiderati.
Si deve notare come la funzione costruita con tale criterio presenta solo un legame lineare con le due variabili Kk e Kp. Se i rettangoli che si utilizzano per l’interpolazione sono sufficientemente ‘piccoli’ l’ipotesi di linearità rimane sostanzialmente valida.
AFFINAMENTO DEL CALCOLO DELLA FEM INDOTTA NELLE SPIRE DI MACCHINA
La possibilità di ricavare il campo al traferro del motore con un analisi bidimensionale agli elementi finiti permette di determinare il valore della fem indotta nelle spire della macchina tenendo anche conto del flusso disperso. L’idea è quella di risalire inizialmente alla fem indotta su di una spira di spessore infinitesimo. Una volta effettuato questo procedimento, si può applicare l’algoritmo per il calcolo della fem su bobine massiccie con il metodo iterativo. Questo algoritmo è stato già costruito in precedenza e viene descritto nel Paragrafo 2.1.1.
Il problema del calcolo della fem indotta in una spira di spessore dx una volta che si conosce l’andamento reale del campo al traferro, è risolvibile con questo criterio:
-
Con la curva del campo al traferro riferita al settore i-esimo della macchina (vedere Paragrafo 2.1) è possibile risalire al flusso che si concatena con una spira posta in qualunque posizione rispetto al passo polare. Per fare questo è sufficiente calcolare l’induzione media al traferro sulla porzione del campo che va a concatenarsi con la spira. Il campo medio al traferro deve essere poi moltiplicato per la superficie della porzione stessa. Ciò che si ottiene da questo prodotto è metà del flusso che si concatena con la spira nel settore ì-esimo (si sta studiando, infatti, l’interazione tra lo statore ed un solo rotore).
Nel Paragrafo 1.3.5 sono state scritte le formule del flusso concatenato sotto l’ipotesi di andamento del campo al traferro rettangolare. In maniera analoga è possibile risalire al valore di Ψ(x) per un andamento generico del campo al traferro. Facendo quindi riferimento alla Figura 1-10b è possibile scrivere:
In questo caso lo spessore Hs risulta essere la differenza tra il raggio massimo ed il minimo del settore i-esimo (Hs=Rmax-Rmin).
-
Il passo successivo per calcolare la fem consiste nel derivare la curva Ψ(x) in modo tale da ottenere la fem indotta. Se si conoscesse la formulazione analitica del flusso concatenato ricavare la fem indotta secondo l’equazione (1.3.5-1) sarebbe elementare. In questo caso, invece, la curva Ψ(x) è solo una funzione tabulata del tipo Ψi=Ψ(xi). Per ricavare la derivata della funzione è quindi necessario effettuare una interpolazione lineare. Vista la necessità di ricavare i valori della derivata prima della funzione è conveniente scegliere il metodo di interpolazione chiamato Cubic Spline. Questo metodo permette di costruire una funzione Ψ’(xi ) del terzo ordine con il vantaggio che la derivata prima risulta essere una funzione del secondo ordine. Le procedure con le quali si effettua l’interpolazione e si calcola la derivata di Ψ( xi) sono state prelevate dalle librerie del linguaggio Fortran (negli allegati sono le procedure spline, splint, dfridr).
Una volta calcolata la fem indotta nella spira di spessore infinitesimo verranno applicati i passaggi: 6.2; 6.3; 6.4 elencati nel Paragrafo 2.1.1. Il calcolo della fem totale indotta nell’intera bobina segue lo stesso processo logico del Paragrafo 2.1.
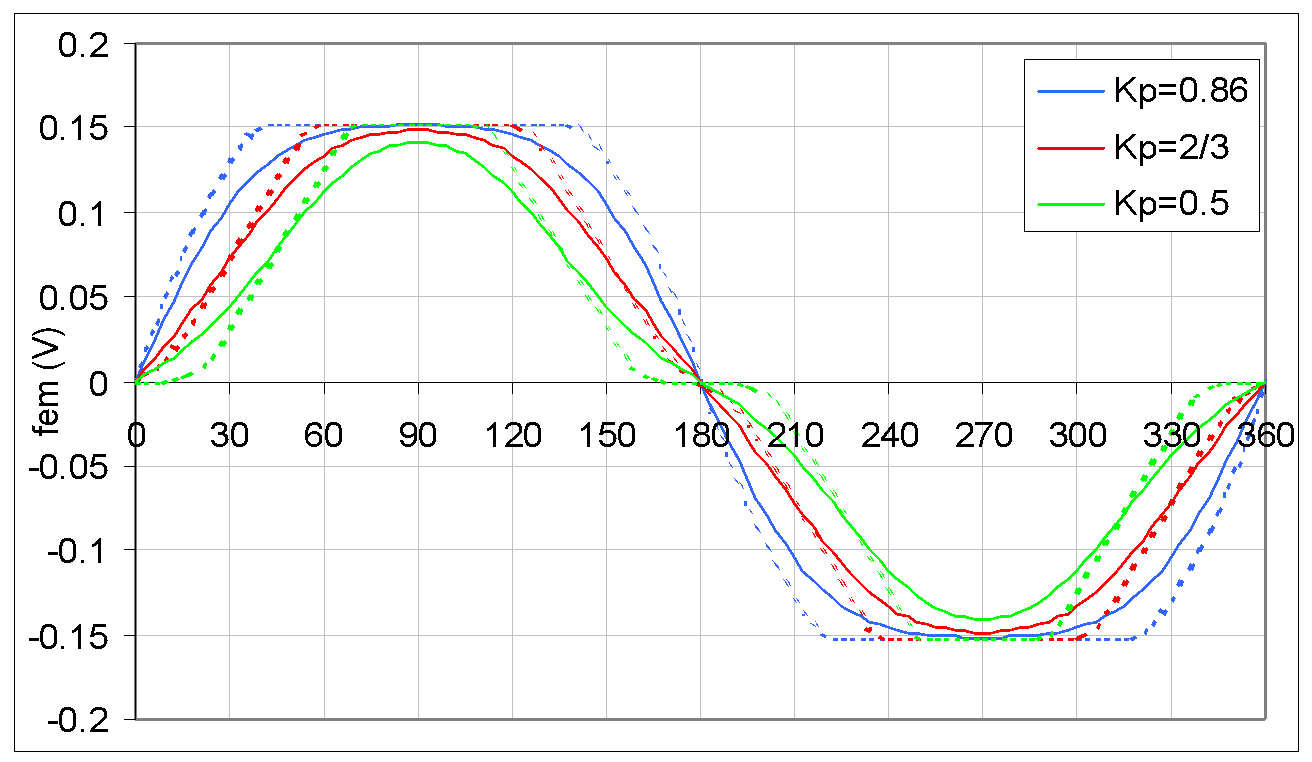
Nelle Figure 5-8, 5-9 sono riportati i profili polari di tre macchine con magneti rettangolari e le relative fem calcolate per una velocità del motore pari a 100 rpm. Nella Figura 5-9 si può apprezzare la differenza tra le fem calcolate con ipotesi di flusso disperso nullo (le curve tratteggiate) e le fem reali calcolate sfruttando la libreria di soluzioni ricavate con il programma agli elementi finiti (le curve con linea continua). Una prima analisi dei grafici evidenzia una riduzione del valore massimo delle fem al decrescere del coefficiente Kp: specie per la curva ricavata dal profilo con Kp=0.5 (tale parametro viene calcolato sul Rmedio) si nota una riduzione considerevole del valore massimo della curva reale rispetto a quello della curva tratteggiata. Questo avviene perché le linee del campo al traferro tendono ad aprirsi facilmente se la superficie occupata dal polo è piccola. In prossimità degli angoli elettrici: 0; 180; e 360 gradi la fem reale è infatti maggiore di quella ideale.
Sempre con riferimento alla Figura 5-9 vengono calcolati i rapporti tra i valori efficaci delle fem calcolate con e senza ipotesi semplificative:
Dai tre valori ottenuti è possibile dedurre che la funzione CVeff(Kp) presenta almeno un punto di massimo per Kp compreso tra 0.5 ed 1.0. I risultati della ricerca del massimo della funzione sono stati i seguenti: per valori di Kp compresi tra 0.64 e 0.72 il parametro CVeff(Kp) è massimo ed assume valori uguali a 0.932÷0.933.
Figura 5-8 Passo polare di un motore a 24 poli con 3 tipi di magneti rettangolari
A questo punto lasciando invariati le dimensioni ed il numero di poli della macchina si eseguono dei calcoli della fem indotta, per tre tipi di magneti trapezoidali. Lo schema dei passi polari della macchina si trova nella Figura 5-10. La forma dei magneti è scelta in modo tale che la retta coincidente con il profilo laterale dei magneti intersechi l’asse della macchina.
La Figura 5-11 riporta le curve delle fem indotte calcolate: anche in questo caso le linee continue rappresentano le fem reali mentre le linee tratteggiate rappresentano le fem calcolate in assenza di flusso disperso. Dalla Figura è possibile notare la differenza sostanziale tra le fem ricavate per Kp=0.5 e per Kp=0.75. Non si evidenziano invece differenze sostanziali quando il passo polare del magnete aumenta da Kp=0.75 a Kp=1.0.
Figura 5-10 Passo polare di un motore a 24 poli con 3 tipi di magneti trapezoidali
Nelle Figure 5-12 e 5-13 sono riportati gli andamenti delle coppia istantanea calcolati per le sei configurazioni di macchina studiate in precedenza. Si è ipotizzata: una corrente di alimentazione di forma sinusoidale; spessore delle bobine in rame pari ad Azcu= 5 mm.
Le coppie rappresentate dalle linee tratteggiate sono ricavate con l’ipotesi di flusso disperso nullo. Le linee continue derivano dalle fem calcolate con lo studio agli elementi finiti del campo al traferro. Gli andamenti ideali delle linee tratteggiate presentano valori della coppia media sempre maggiori di quelli reali. E’ evidente inoltre che le componenti armoniche della coppia pulsante tendono a diminuire nel caso reale, quando si tiene conto del flusso disperso.
Figura 5-11 Grafico delle fem indotte sui tre motori della Fig.5-10 (n=100 rpm)
Dalla Figura 5-13 è possibile notare la differenza sostanziale tra la coppia reale ricavata per Kp=0.5 e per Kp=0.75. Non si evidenziano invece differenze sostanziali quando il passo polare del magnete aumenta da Kp=0.75 a Kp=1.0.
Figura 5-12 Coppia istantanea per le configurazioni della Figura 5-8 con magneti rettangolari
Figura 5-13 Coppia istantanea per le configurazioni della Figura 5-10 con magneti trapezoidali
-
OTTIMIZZAZIONE DI UN MOTORE CON MINIMIZZAZIONE DEL
PESO E DELLA COPPIA PULSANTE
In questo paragrafo si eseguirà un ottimizzazione di un motore con le seguenti specifiche:
-
Alla velocità di 210 rpm la coppia di macchina deve essere tale che Tm≥220 [Nm].
-
Il rendimento del motore non deve essere inferiore al 93 %.
-
Il raggio di ingombro della macchina deve essere minore di 250 mm.
-
La frequenza di funzionamento può variare tra 40 e 60 Hz.
-
La sovratemperatura ΔT rispetto alla temperatura ambiente (Ta=35 [°C]) vale 60 [°C].
-
La corrente di alimentazione del motore presenta una forma d’onda sinusoidale.
Le funzioni obiettivo dell’ottimizzazione da effettuare, sono: la funzione peso delle parti attive della macchina; la funzione valore efficace della coppia pulsante della macchina.
I magneti in Neodimio-Ferro-Boro utilizzati presentano un campo coercitivo pari a 800 [kA/m] ed un’induzione residua pari a 1.3 [T].
Il calcolo delle fem indotte nei diversi progetti che verranno effettuati dal sistema di ottimizzazione, avverrà con il criterio spiegato nei paragrafi precedenti di questo Capitolo. Nella Tabella 5-3 viene riportata l’ottimizzazione del peso del motore effettuata all’inizio con il metodo delle direzioni coordinate e nella fase finale con il metodo di Box.
Tabella 5-3 Ottimizzazione del peso del motore con specifiche su coppia e rendimento
|
Rest |
Kr |
Poli |
Kpest |
Kpint |
Azcu |
Tm |
m |
Peso |
Perdite |
Jt |
|
|
Unità |
[mm] |
[mm] |
[Nm] |
[kg] |
[W] |
A/mm2 |
|||||
|
Metodo delle direzioni coordinate |
|||||||||||
|
0 |
150 |
0.8 |
26 |
0.7 |
0.7 |
5 |
33.5 |
88.4 |
7.5 |
96.5 |
3.54 |
|
1 |
238 |
0.5 |
26 |
0.7 |
0.7 |
5 |
263 |
91.3 |
38.7 |
550 |
4.76 |
|
2 |
238 |
0.71 |
26 |
0.7 |
0.7 |
5 |
220 |
92.7 |
29.5 |
379 |
4.1 |
|
3 |
238 |
0.71 |
22.9 |
0.7 |
0.7 |
5 |
225 |
92.9 |
31.6 |
379 |
4.12 |
|
4 |
238 |
0.71 |
22.9 |
0.76 |
0.7 |
5 |
229 |
93 |
32.8 |
379 |
4.09 |
|
5 |
238 |
0.71 |
22.9 |
0.76 |
0.7 |
5 |
229 |
93 |
32.8 |
379 |
4.09 |
|
6 |
238 |
0.73 |
22.9 |
0.76 |
0.7 |
5 |
220 |
93.1 |
31.5 |
361 |
4.04 |
|
Metodo di Box |
|||||||||||
|
1 |
238 |
0.73 |
22 |
0.76 |
0.7 |
5 |
221 |
93.1 |
32.2 |
361 |
4.04 |
La macchina utilizzata come progetto iniziale dell’ottimizzazione non rispetta nessuna delle due specifiche di progetto imposte ((m=88.4% Tm=33.5 [Nm]). Il sistema di ottimizzazione lineare, nella 1° iterazione riesce a produrre una macchina con coppia pari a 263 [Nm]. La specifica progettuale sulla coppia è ampiamente soddisfatta, variando semplicemente il raggio esterno della macchina. Il rendimento nella 1° iterazione è del 91.3%, di conseguenza il sistema, comincia a lavorare per soddisfare la seconda specifica di progetto. Infatti, nella 2° iterazione viene variato il raggio interno della macchina riducendo lo spessore della corona rotorica. Il fattore Kr viene elevato dal valore 0.5 al valore 0.71. La specifica sul rendimento viene ottenuta anche riducendo il numero di poli di macchina. In pratica, dopo poche modifiche della configurazione geometrica il sistema raggiunge una macchina che soddisfa le due specifiche su coppia e rendimento. Ovviamente il sistema per raggiungere un buon rendimento tende a produrre una motore con coppia minore dei 263[Nm] inizialmente raggiunti (nella 4° iterazione, la coppia viene infatti ridotta al limite ammissibile di 220 [Nm]).
Soddisfatte le due specifiche di progetto il sistema comincia ad ottimizzare la funzione di prestazione di interesse: il peso delle parti attive della macchina. Si nota che il metodo delle direzioni coordinate, dalla 4° iterazione in poi non riesce a ridurre notevolmente il peso della macchina. Questo avviene perché la minimizzazione di una funzione sottoposta a dei vincoli strutturali, dimensionali e di progetto può avvenire lungo le direzioni più disparate dello spazio (n+1)-dimensionale. Il metodo di Box oltre a raggiungere un risultato di macchina reale (con numero di poli intero) permette lo spostamento delle variabili geometriche in tutte le possibili direzioni dello spazio.
Dalla Tabella 5-3 si osserva che la macchina di peso minimo viene ottenuta con il metodo evoluzionistico dopo 8 iterazioni. E’ interessante notare come il sistema abbia ridotto il numero di poli ( p=22 ) durante la massimizzazione del rendimento mentre abbia poi aumentato nuovamente questa grandezza ( p=26 ) per ridurre il peso delle parti attive. Come già osservato nelle minimizzazioni del peso del Capitolo quattro, il sistema varia la forma dei magneti aumentandone lo spessore occupato sul passo polare in prossimità del raggio esterno della macchina.
Nella Figura 5-14 si riporta il profilo della coppia di macchina lungo 360° elettrici. Oltre alla componente del valore medio è possibile apprezzare delle componenti armoniche della coppia (sesta, dodicesima, etc…). Le componenti armoniche non contribuiscono alla produzione di potenza meccanica ma creano solo problemi di vibrazione. Si vuole eseguire una nuova ottimizzazione cercando di spianare la curva della coppia minimizzando il ‘valore efficace’ della coppia pulsante.
Le specifiche sulla coppia ed il rendimento di macchina sono lasciate invariate, mentre si impone che il peso della parti attive non superi i 31.6 kg. In pratica, si lascia un margine di modifica del peso di 2 kg rispetto alla macchina di peso minimo trovata nella Tabella 5-3.
Nella Tabella 5-4 viene riportato il solo risultato finale dell’ottimizzazione della coppia pulsante effettuata. Dal risultato ottenuto si osserva che il sistema di elaborazione ha fatto crescere lo spessore della bobina e la superficie dei magneti. Oltre alla riduzione delle componenti armoniche della coppia si può apprezzare un guadagno sul rendimento della macchina. Il peso della parti attive della macchina è stato portato sul limite consentito dall’ultimo vincolo applicato.