In questo articolo si riportano vari esempi di processi di ottimizzazione. Si vogliono affrontare i vari tipi di esigenze che possono presentarsi nella realtà quando esistono delle specifiche di progetto e si desidera ottenere delle prestazioni ben definite.
L’ottimizzazione verrà effettuata non tenendo conto del problema dello stipamento dei conduttori: la bobina di macchina si ipotizza costituita da un unico conduttore massiccio. Effettuare il progetto di macchina considerando le bobine costituite da conduttori reali permette di calcolare con un errore minore le seguenti grandezze: perdite addizionali nel rame; il raggio di ingombro Ring; la reale lunghezza delle testate di macchina; le perdite per effetto Joule nel rame; il peso delle bobine. Queste grandezze possono essere calcolate perché, una volta scelto il conduttore si possono ricavare le sue dimensioni ed il raggio di curvatura.
Affrontare l’ottimizzazione di una macchina a disco con bobine reali presenta un problema molto evidente: se non si tiene conto delle caratteristiche del convertitore che deve essere abbinato alla macchina, l’algoritmo converge sempre su di un progetto nel quale si prevede l’avvolgimento del conduttore più piccolo disponibile. Questo avviene perché la riduzione della sezione del conduttore per la macchina a disco offre una serie di vantaggi:
– aumenta lo stipamento del rame per la sezione disponibile per la bobina
– diminuiscono le perdite addizionali con il quadrato dello spessore del conduttore
– diminuisce la lunghezza delle testate perché si riduce il raggio di curvatura.
Tuttavia, non sarà sempre possibile realizzare macchine con questa caratteristica perché i convertitori che le alimentano normalmente hanno tensioni nominali che non superano il centinaio di V. Questo vincolo potrebbe essere comunque rispettato effettuando parecchie connessioni in parallelo tra le fasi del motore. E’ ovvio però che anche questa strada crea molti problemi nella costruzione delle connessioni delle bobine.
In conclusione, la soluzione migliore di un’ottimizzazione deve tenere conto anche dei problemi di costruzione della macchina. Questo in pratica vuol dire che, una volta scelto il tipo di conduttore ed il numero di strati Nst delle bobine, bisogna controllare se almeno uno dei quattro tipi di collegamento della Figura 1-18 produce tensioni di macchina accettabili per il convertitore che dovrà essere collegato. Se questo non dovesse avvenire il progetto dovrebbe essere scartato.
E’ probabile, in ogni modo, che durante un’ottimizzazione, il vincolo sulla tensione arresti soltanto il rimpicciolimento dei conduttori. In generale, per la macchina migliore verrà scelto sempre un conduttore con collegamento tra le bobine stella-serie (Figura 1-18) e tensione nominale di macchina poco al di sotto della tensione massima di funzionamento del convertitore.
L’affinamento della macchina con l’introduzione di avvolgimenti reali della bobina, non è importante perché si desidera conoscere il valore di queste due grandezze, ma perché nella fase finale della progettazione si vuole sempre ricavare dei risultati che si discostano il meno possibile da quelli reali.
Tutte le ottimizzazioni effettuate subiranno i seguenti vincoli strutturali:
– I rapporti Kpest, Kpint saranno sempre minori di 0.85
– Lo spessore della bobina lungo l’asse z (Azcu) non supererà mai 7.5 mm
Se queste condizioni non venissero rispettate l’errore sui risultati dovuto alle ipotesi di flussi dispersi nulli diventerebbe elevato.
4.2 Ottimizzazioni della coppia media del motore.
In questo paragrafo si svolgeranno delle ottimizzazioni della coppia meccanica dei motori a disco. Nell’impostazione del problema non verrà posta alcuna specifica sulle altre funzioni di prestazione. Questa scelta è stata fatta per lasciare piena libertà di variazione strutturale del motore. Si vuole anche controllare il legame che la funzione obiettivo presenta rispetto alle altre grandezze.
Lo studio di questa problematica deve avvenire necessariamente fissando il vincolo dimensionale sul raggio di ingombro. Se non si ponesse questa condizione il risultato della massimizzazione sarebbe una macchina di raggio infinito.
Nella Tabella 4-1 vengono riassunti i passaggi di un’ottimizzazione con i seguenti dati:
– Il raggio di ingombro prescelto per la macchina vale Ring=240mm
– La velocità di rotazione del motori viene fissata pari a 200 rpm
– La temperatura massima di funzionamento vale 100 °C.
– I motori vengono alimentati con corrente avente forma d’onda sinusoidale e frequenza variabile tra i 40 ed i 60 Hz.
Tabella 4-1 Iterazioni per l’ottimizzazione della coppia media di macchina (Raggio di ingombro= 240 mm)
| Iterazione | Rest | Kr | Poli | Kpest | Kpint | Azcu | Tm (P) | hm | Peso | Perdite | Jt |
| Unità [mm] [mm] [Nm] [kg] [W] [A/mm2]
Metodo di Powell |
|||||||||||
| 1 | 60 | 0.67 | 24 | 0.7 | 0.7 | 3 | 2.1 | 66.6 | 1.22 | 21.9 | 4.95 |
| 2 | 60 | 0.67 | 24 | 0.7 | 0.7 | 7.5 | 3.7 | 78 | 1.93 | 21.9 | 3.22 |
| 3 | 60 | 0.67 | 24 | 0.7 | 0.85 | 7.5 | 3.9 | 78.7 | 2.05 | 21.9 | 3.2 |
| 5 | 60 | 0.67 | 24 | 0.85 | 0.85 | 7.5 | 4 | 79.4 | 2.22 | 21.9 | 3.17 |
| 10 | 60 | 0.67 | 26.8 | 0.85 | 0.85 | 7.5 | 4.1 | 79.5 | 2.16 | 21.9 | 3.15 |
| 17 | 60 | 0.54 | 26.8 | 0.85 | 0.85 | 7.5 | 4.4 | 77.2 | 2.46 | 27.3 | 3.5 |
| 20 | 60 | 0.54 | 26.8 | 0.85 | 0.85 | 7.5 | 4.4 | 77.2 | 2.46 | 27.3 | 3.5 |
| 30 | 60 | 0.53 | 26.6 | 0.85 | 0.85 | 7.5 | 4.4 | 77.2 | 2.47 | 27.4 | 3.51 |
| 33 | 226 | 0.14 | 26.6 | 0.85 | 0.85 | 7.5 | 201 | 84.9 | 49.1 | 748 | 7.52 |
| 64 | 226 | 0.14 | 26.6 | 0.85 | 0.85 | 7.5 | 201 | 84.9 | 49.1 | 748 | 7.52 |
| Metodo di Box | |||||||||||
| 1 | 226 | 0.16 | 26 | 0.85 | 0.85 | 7.5 | 222 | 86.1 | 50.4 | 747 | 7 |
| 2 | 226 | 0.19 | 26 | 0.85 | 0.85 | 7.5 | 241 | 87.1 | 51.2 | 746 | 6.59 |
| 3 | 226 | 0.23 | 26 | 0.85 | 0.85 | 7.5 | 274 | 88.6 | 52.5 | 740 | 5.97 |
| 4 | 226 | 0.28 | 24 | 0.85 | 0.85 | 7.5 | 302 | 89.6 | 55.4 | 731 | 5.53 |
| 5 | 226 | 0.32 | 24 | 0.85 | 0.85 | 7.5 | 325 | 90.5 | 56.1 | 718 | 5.2 |
| 6 | 226 | 0.36 | 24 | 0.85 | 0.85 | 7.5 | 343 | 91.1 | 56.6 | 701 | 4.93 |
| 6 | 226 | 0.41 | 24 | 0.85 | 0.85 | 7.5 | 356 | 91.6 | 56.6 | 680 | 4.7 |
| 7 | 226 | 0.45 | 24 | 0.85 | 0.85 | 7.5 | 364 | 92.1 | 56.4 | 655 | 4.51 |
| 8 | 226 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 367 | 92.5 | 55.8 | 627 | 4.35 |
Dalla Tabella si osserva l’evoluzione del progetto che porta alla costruzione di motori con coppia nominale sempre più elevata. La soluzione viene raggiunta con due metodi in cascata quello di Powell e quello di Box. Il metodo di Powell si arresta alla 64° iterazione con un rapporto Kr (Kr=0.14) molto lontano da quello della soluzione finale. Questo avviene perché alla condizione di arresto del metodo di Powell viene assegnato un errore elevato. Infatti, con questo metodo si ottiene comunque una macchina irrealizzabile perché il numero di coppie di poli è decimale. Per questo motivo, non ha quindi senso imporre una precisione della soluzione finale elevata. Il vantaggio nell’applicare comunque il metodo di Powell può essere rilevato osservando che nell’ultima soluzione ( la 64°), quattro delle sei variabili in gioco risultano uguali alla soluzione finale fornita dal metodo di Box.
Nella Tabella 4-2 vengono riportati i risultati di alcune ottimizzazioni effettuate al variare del raggio di ingombro.
Tabella 4-2 Ottimizzazione della coppia media al variare del raggio di ingombro del motore
| Ring | Rest | Kr | Poli | Kpest | Kpint | Azcu | Tm (P) | hm | Peso | Perdite | Jt | |
| Unità | [mm] | [mm] | [Nm] | [kg] | [W] | A/mm2 | ||||||
| 80 | 68.5 | 0.53 | 26 | 0.85 | 0.85 | 7.5 | 6 | 78.8 | 3.02 | 33.8 | 3.56 | |
| 100 | 85.5 | 0.52 | 24 | 0.85 | 0.85 | 7.5 | 14.9 | 83.1 | 5.63 | 63.7 | 3.73 | |
| 120 | 106 | 0.51 | 24 | 0.85 | 0.85 | 7.5 | 30.2 | 85.8 | 9.14 | 105 | 3.86 | |
| 140 | 126 | 0.51 | 24 | 0.85 | 0.85 | 7.5 | 53.9 | 87.7 | 13.7 | 159 | 3.97 | |
| 160 | 146 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 87.8 | 89.1 | 19.4 | 225 | 4.07 | |
| 180 | 166 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 134 | 90.2 | 26.4 | 305 | 4.16 | |
| 200 | 186 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 194 | 91.1 | 34.7 | 397 | 4.22 | |
| 220 | 206 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 271 | 91.9 | 44.4 | 504 | 4.28 | |
| 240 | 226 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 367 | 92.5 | 55.8 | 627 | 4.35 | |
| 260 | 246 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 483 | 93 | 68.8 | 764 | 4.41 | |
| 280 | 266 | 0.49 | 24 | 0.85 | 0.85 | 7.5 | 622 | 93.4 | 83.6 | 917 | 4.46 | |
| 300 | 286 | 0.49 | 24 | 0.85 | 0.85 | 7.5 | 785 | 93.8 | 100 | 1087 | 4.51 | |
| 320 | 306 | 0.49 | 24 | 0.85 | 0.85 | 7.5 | 976 | 94.2 | 119 | 1269 | 4.55 | |
Dai risultati ottenuti si osserva che:
– Il fattore Kr vale all’incirca 0.5 per tutte le ottimizzazioni effettutate. Si può notare come questo parametro tende a diminuire leggermente con l’aumento del raggio di ingombro delle macchine
– Tranne la soluzione con raggio di ingombro pari a 80 mm, il numero di poli scelto è sempre il minore possibile (frequenza minima pari a 40 Hz). La spiegazione di questo andamento viene data nel paragrafo successivo.
– I magneti sono trapezoidali è la superficie rotorica che occupano è la massima ammissibile dai vincoli imposti nel Paragrafo 4-1.
– La sezione del rame sfruttabile è la massima ammissibile.
– Per le macchine con raggio di ingombro elevato i valori del rendimento sono soddisfacenti.
4.3 OTTIMIZZAZIONE DEL RENDIMENTO E DELLA COPPIA DEL MOTORE
Si suppone che un progetto A presenti le seguenti specifiche:
– Convertitore che fornisce una corrente con forma d’onda sinusoidale
– Raggio di ingombro Ring = 250 mm
– Frequenza di funzionamento tra 40 – 60 Hz
– Sovratemperatura DT = 50 ° C
– Temperatura ambiente Ta = 35 ° C
– La coppia di macchina a 240 rpm deve assumere un valore maggiore o uguale di Tm = 200 [Nm]
Si desidera costruire una macchina che soddisfi queste condizioni e che abbia rendimento massimo.
Il problema che si deve affrontare rientra nella categoria delle ottimizzazioni monobiettivo con vincoli: la soluzione del problema viene riassunta nella Tabella 4-3.
| Rest | Kr | Poli | Kpest | Kpint | Azcu | hm(P) | Tm | Peso | Perdite | Jt | |
| Unità [mm] [mm] [Nm] [kg] [W] [A/mm2] | |||||||||||
| Powell | |||||||||||
| 1 | 150 | 0.73 | 24 | 0.7 | 0.7 | 3 | 86.47 | 42.78 | 10.41 | 139.6 | 5.45 |
| 16 | 150 | 0.73 | 20 | 0.85 | 0.85 | 7.5 | 91.88 | 73.67 | 18.59 | 139.6 | 3.33 |
| 17 | 150 | 0.77 | 20 | 0.85 | 0.85 | 7.5 | 91.19 | 64.1 | 17.4 | 121 | 3.19 |
| 70 | 150 | 0.78 | 21.4 | 0.85 | 0.85 | 7.5 | 91.92 | 63.69 | 16.62 | 119 | 3.21 |
| 71 | 235.5 | 0.49 | 21.4 | 0.85 | 0.85 | 7.5 | 93.6 | 417.03 | 65.6 | 622.96 | 4.2 |
| 95 | 235.5 | 0.50 | 19.2 | 0.85 | 0.85 | 7.5 | 93.6 | 413.5 | 69.34 | 619.8 | 4.23 |
| Box | |||||||||||
| 1 | 235.5 | 0.52 | 20 | 0.85 | 0.85 | 7.5 | 93.8 | 413.6 | 67.44 | 604.9 | 4.18 |
| 2 | 235.5 | 0.54 | 20 | 0.85 | 0.85 | 7.5 | 93.8 | 410.8 | 66.9 | 588 | 4.11 |
| 3 | 235.5 | 0.57 | 20 | 0.85 | 0.85 | 7.5 | 93.9 | 406.5 | 66.27 | 570.2 | 4.05 |
| 4 | 235.5 | 0.58 | 20 | 0.85 | 0.85 | 7.5 | 94 | 400.6 | 65.54 | 550.5 | 3.98 |
| 5 | 235.5 | 0.60 | 20 | 0.85 | 0.85 | 7.5 | 94.1 | 393.1 | 64.72 | 530.9 | 3.92 |
| 6 | 235.5 | 0.63 | 20 | 0.85 | 0.85 | 7.5 | 94.2 | 384 | 63.8 | 510.3 | 3.86 |
| 7 | 235.5 | 0.65 | 20 | 0.85 | 0.85 | 7.5 | 94.3 | 373.3 | 62.78 | 489.8 | 3.8 |
| 8 | 235.5 | 0.67 | 20 | 0.85 | 0.85 | 7.5 | 94.3 | 360.8 | 61.67 | 454.4 | 3.74 |
| 9 | 235.5 | 0.67 | 20 | 0.85 | 0.85 | 7.5 | 94.4 | 346.7 | 60.45 | 432 | 3.67 |
macchina praticamente si dimezzano mentre la coppia (in pratica la potenza) di macchina diminuisce solo del 36%.
6) Visti i vincoli sulla frequenza di funzionamento (il numero di poli della macchina poteva variare tra 20 e 30), il progetto migliore presenta un numero di poli pari a 22 perché evidentemente con questo valore è stato raggiunto un compromesso tra le perdite nel ferro e nel rame e le perdite per effetto Joule alle testate degli avvolgimenti.
La soluzione di questa ottimizzazione presenta un difetto perché la macchina può fornire più coppia ((Tm = 77 [Nm]) di quella che le viene richiesta al limite termico assegnato. Riducendo la corrente introdotta nella macchina si trova che questa fornisce una coppia pari a 200 [Nm] nelle seguenti condizioni:
Tabella 4-4 Funzionamento del motore A alla temperatura di 60° C
| Tf | rendimento | Tm | Perdite | Jt |
| [°C] | [Nm] | [W] | [A/mm2] | |
| 60 | 95.98 | 200.0 | 183.6 | 2.44 |
Come si può osservare il rendimento della macchina sale ulteriormente quando la densità di corrente fornita diminuisce. Bisogna ricordare che le perdite per effetto Joule diminuiscono con il quadrato della corrente. Inoltre, al diminuire delle perdite della macchina si riduce la temperatura di funzionamento e quindi diminuisce la resistenza dei conduttori.
Utilizzare un motore elettrico ad una temperatura minore di quella ammissibile vuol dire sicuramente non sfruttarne al massimo la potenzialità. Se comunque si desidera aumentare ulteriormente il rendimento è possibile introdurre la temperatura di funzionamento come una variabile delle funzioni di prestazione. La funzione obiettivo diventerà quindi dipendente da sette grandezze:
F(P) = F (Rest, Rint, poli, Kpest, Kpint, Azcu, Tf )
La soluzione del progetto B è avvenuta utilizzando il metodo delle direzioni coordinate ed il metodo di Box.
Nella Tabella 4-5 si osserva che le funzioni di penalità su F(P) vengono applicate fino alla 113° iterazione. Siccome ci sono sette variabili in gioco il numero delle direzioni di ottimizzazione ammissibili è molto elevato. Il metodo di Box infatti, entra in funzione solo dopo 260 iterazioni.
Analizzando la soluzione B appena ottenuta si possono effettuare i seguenti rilievi:
– La temperatura di funzionamento di questa macchina vale appena 48°C; la sovratemperatura è bassissima ((T = 13.2 ° C ).
– La coppia media è stata portata sul limite ammissibile. In pratica, viene impressa la corrente strettamente necessaria per produrla Jeff = 2 [A/mm2].
– Il numero dei poli è il minimo possibile. Le perdite nel ferro e quelle addizionali nel rame sono minimizzate scegliendo una frequenza di alimentazione minima.
– Il rapporto Kr è basso rispetto al risultato della Tabella 4-3 (0.65 contro 0.77) perché a parità di corrente, si vuole sfruttare la massima superficie per lo scambio delle forze tra statore e rotore.
- Dal momento in cui la coppia rimane al di sopra dei 200 [Nm] il peso della macchina aumenta costantemente. Questa macchina pesa 10 kg in più rispetto alla precedente.
Tabella 4-5 Ottimizzazione di un motore B di elevato rendimento
| Rest | Kr | Poli | Kpest | Kpint | Azcu | Tf | hm(P) | Tm | Peso | Perdite | Jt | |
| Unità | [mm] | [mm] | [Nm] | [Nm] | [kg] | [W] | A/mm2 | |||||
| Direzioni coordinate | ||||||||||||
| 10 | 180 | 0.83 | 24 | 0.7 | 0.7 | 3 | 50 | 3.1 | 31.3 | 14.3 | 58.7 | 2.84 |
| 51 | 180 | 0.51 | 28.8 | 0.85 | 0.85 | 7.5 | 90 | 17.8 | 178 | 29.9 | 369 | 4.18 |
| 113 | 206 | 0.44 | 28.8 | 0.85 | 0.85 | 7.5 | 60.6 | 94.1 | 200 | 42.1 | 288 | 3.2 |
| 147 | 224 | 0.49 | 28.8 | 0.85 | 0.85 | 7.5 | 48.9 | 95.4 | 200 | 50.6 | 224 | 2.35 |
| 215 | 224 | 0.51 | 28.8 | 0.85 | 0.85 | 7.5 | 48.9 | 95.4 | 200 | 50.2 | 220 | 2.31 |
| 260 | 233 | 0.49 | 26.1 | 0.85 | 0.85 | 7.5 | 45.7 | 95.9 | 200 | 58.1 | 196 | 2.07 |
| Box | ||||||||||||
| 1 | 233 | 0.51 | 24 | 0.85 | 0.85 | 7.5 | 50.7 | 95.6 | 237 | 60 | 235 | 2.43 |
| 2 | 233 | 0.53 | 22 | 0.85 | 0.85 | 7.5 | 50.7 | 95.5 | 235 | 62.1 | 221 | 2.38 |
| 3 | 233 | 0.56 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 95.7 | 231 | 64.7 | 208 | 2.32 |
| 4 | 233 | 0.58 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 95.9 | 228 | 64 | 202 | 2.28 |
| 5 | 233 | 0.6 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 95.9 | 224 | 63.2 | 196 | 2.25 |
| 6 | 233 | 0.62 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 96 | 219 | 62.4 | 189 | 2.21 |
| 7 | 233 | 0.64 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 96 | 213 | 61.4 | 183 | 2.18 |
| 8 | 233 | 0.66 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 96.1 | 207 | 60.4 | 175 | 2.14 |
| 9 | 233 | 0.66 | 20 | 0.85 | 0.85 | 7.5 | 50.7 | 96.1 | 207 | 60.4 | 175 | 2.14 |
| 10 | 235 | 0.65 | 20 | 0.85 | 0.85 | 7.5 | 48.2 | 96.2 | 201 | 62.9 | 164 | 2 |
I costi di funzionamento della macchina B sono molto ridotti. E’ facile però comprendere che il costo di produzione è invece elevato: il peso del rame, del ferro e dei magneti permanenti potrebbe essere sfruttato per costruire motori con coppie nominali ben al di sopra dei 200 [Nm] e con rendimenti più che accettabili. Nella Tabella 4-6 viene riportato un progetto di una macchina C che ha le stesse specifiche del progetto A. La differenza che viene introdotta consiste nel vincolare la coppia media tra 200 [Nm] e 210 [Nm].
La differenza evidente che la macchina C presenta rispetto alle macchine A e B è l’elevato rapporto tra i raggi (Kr=0.84). Il rendimento è comunque al di sopra del 94%.
Tabella 4-6 Ottimizzazione della macchina C
| Rest | Kr | Poli | Kpest | Kpint | Azcu | hm(P) | Tm | Peso | Perdite | Jt | |
| Unità [mm] [mm] [Nm] [kg] [W] [A/mm2] | |||||||||||
| Powell | |||||||||||
| 1 | 150 | 0.73 | 24 | 0.7 | 0.7 | 3 | 86.5 | 42.8 | 10.4 | 154 | 5.45 |
| 10 | 150 | 0.73 | 28.8 | 0.85 | 0.85 | 7.5 | 91.7 | 77.2 | 15.6 | 161 | 3.48 |
| 20 | 150 | 0.51 | 28.8 | 0.85 | 0.85 | 7.5 | 90.8 | 98.4 | 19.5 | 242 | 4.07 |
| 30 | 150 | 0.51 | 28.8 | 0.85 | 0.85 | 7.5 | 90.4 | 98.4 | 19.5 | 242 | 4.07 |
| 40 | 207 | 0.37 | 28.8 | 0.85 | 0.85 | 4.7 | 89.3 | 205 | 35.5 | 565 | 6.01 |
| 50 | 207 | 0.37 | 27.7 | 0.85 | 0.85 | 4.8 | 89.4 | 205 | 36.2 | 557 | 5.94 |
| 57 | 207 | 0.37 | 27.7 | 0.85 | 0.85 | 4.8 | 89.4 | 205 | 36.2 | 557 | 5.94 |
| Box | |||||||||||
| 1 | 202 | 0.4 | 24 | 0.85 | 0.85 | 5.3 | 90.3 | 204 | 37.7 | 505 | 5.43 |
| 4 | 196 | 0.65 | 20 | 0.85 | 0.85 | 7.4 | 93.3 | 205 | 39.2 | 341 | 3.74 |
| 7 | 203 | 0.72 | 20 | 0.85 | 0.85 | 7.4 | 93.7 | 203 | 40.3 | 318 | 3.56 |
| 8 | 206 | 0.74 | 20 | 0.85 | 0.85 | 7.4 | 93.8 | 200 | 40.5 | 307 | 3.5 |
| 9 | 209 | 0.75 | 20 | 0.85 | 0.85 | 7.4 | 93.9 | 202 | 41.5 | 304 | 3.45 |
| 10 | 213 | 0.77 | 20 | 0.85 | 0.85 | 7.4 | 94 | 203 | 42.4 | 300 | 3.4 |
| 11 | 217 | 0.79 | 20 | 0.85 | 0.85 | 7.4 | 94.1 | 202 | 43.4 | 295 | 3.36 |
| 12 | 222 | 0.8 | 20 | 0.85 | 0.85 | 7.4 | 94.1 | 203 | 44.9 | 291 | 3.3 |
| 13 | 227 | 0.82 | 20 | 0.85 | 0.85 | 7.4 | 94.2 | 203 | 46.4 | 286 | 3.25 |
| 14 | 232 | 0.83 | 22 | 0.85 | 0.85 | 7.4 | 94.3 | 205 | 44.8 | 284 | 3.25 |
| 15 | 236 | 0.85 | 24 | 0.85 | 0.85 | 7.4 | 94.3 | 203 | 42.9 | 278 | 3.24 |
| 16 | 236 | 0.84 | 22 | 0.85 | 0.85 | 7.4 | 94.4 | 203 | 45.9 | 278 | 3.19 |
Nella Figura 4-1 si riportano gli schemi del passo polare delle tre macchine appena studiate con i relativi risultati ottenuti.
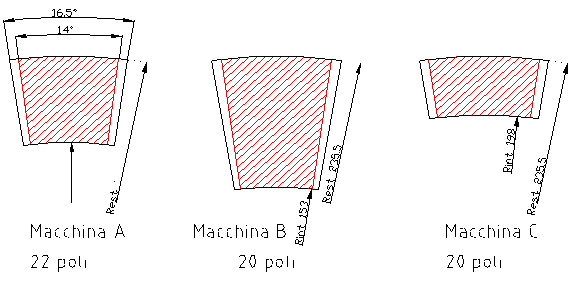
I vantaggi offerti dalla macchina C sono evidenti:
1) Il costo di produzione di questa macchina sarà sicuramente minore di quello delle altre due.
2) La macchina C presenta un peso delle parti calcolabili minore di 6 kg della macchina A e minore di 15 kg della macchina B.
Fino ad ora la coppia media del motore è stata una specifica del progetto. Mantenendo i vincoli dimensionali e tutti i dati introdotti all’inizio del Paragrafo, si cambiano gli obiettivi di ottimizzazione in questo modo:
1) Il Rendimento del motore deve essere superiore al 94 %
2) La funzione di prestazione da ottimizzare è la coppia media di macchina.
In pratica, si inverte il problema cercando di costruire un motore di maggiore potenza con rendimento elevato.
Per risolvere il problema si deve eseguire di nuovo un’ottimizzazione con vincoli sia dimensionali che di prestazione. Evidentemente la temperatura di funzionamento del motore può essere mantenuta costante durante tutta l’ottimizzazione. Per massimizzare la coppia il sistema sceglierà, infatti, la massima corrente ammissibile al limite termico.
Nella Tabella 4-7 sono riportate le iterazioni dell’ottimizzazione D. Viste le condizioni iniziali l’algoritmo entra nei vincoli di progetto immediatamente. Osservando la soluzione si possono trarre le seguenti conclusioni:
– Il motore ottenuto occupa tutto l’ingombro radiale disponibile.
– Il rapporto Kr è molto basso. La lunghezza dei lati attivi del motore è molto elevata (Hs = 118 mm ). Il sistema di ottimizzazione ha fatto crescere lo spessore radiale della corona circolare fino a quando il rendimento è rimasto sopra i valori accettabili.
– Il numero di poli della macchina è il minimo possibile considerando le condizioni sulla frequenza di alimentazione (tra 40 e 60 Hz). Si può comunque notare, che l’ultima macchina a 24 poli calcolata con il metodo di Box nella 2° iterazione, presenta una coppia pari a 376 [Nm]; appena 16 [Nm] più bassa della soluzione finale.
Dalla Tabella si osserva che una macchina di queste dimensioni che ruota a 240 rpm alla temperatura di 90 °C, può smaltire circa 0.5 kW. Ridurre il numero di poli vuol dire abbassare le perdite nel ferro e le perdite addizionali nel rame, con il vantaggio di poter aumentare le perdite per effetto Joule. Quindi un margine maggiore sulle perdite nel rame permette di innalzare la corrente aumentando la potenza del motore.
Tabella 4-7 Ottimizzazione della macchina D
| Rest | Kr | Poli | Kpest | Kpint | Azcu | T(P) | hm | Peso | Perdite | Jt | |
| Unità [mm] [mm] [Nm] [kg] [W] [A/mm2] | |||||||||||
| Powell | |||||||||||
| 1 | 200 | 0.75 | 24 | 0.7 | 0.7 | 3 | 90.5 | 90.5 | 21.5 | 229 | 5.01 |
| 5 | 200 | 0.75 | 24 | 0.85 | 0.85 | 7.5 | 163 | 94.3 | 33.6 | 229 | 3.11 |
| 10 | 200 | 0.75 | 24 | 0.85 | 0.85 | 7.5 | 163 | 94.3 | 33.7 | 229 | 3.11 |
| 15 | 200 | 0.75 | 24 | 0.85 | 0.85 | 7.5 | 163 | 94.3 | 33.7 | 229 | 3.11 |
| 20 | 200 | 0.65 | 24 | 0.85 | 0.85 | 7.5 | 203 | 94 | 38 | 299 | 3.38 |
| 25 | 200 | 0.65 | 24 | 0.85 | 0.85 | 7.5 | 203 | 94 | 38 | 299 | 3.38 |
| 30 | 200 | 0.65 | 24 | 0.85 | 0.85 | 7.5 | 203 | 94 | 38 | 299 | 3.38 |
| 55 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| 60 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| 61 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| 62 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| Box | |||||||||||
| 1 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| 2 | 236 | 0.55 | 24 | 0.85 | 0.85 | 7.5 | 376 | 94.4 | 60.8 | 514 | 3.73 |
| 3 | 236 | 0.53 | 20 | 0.85 | 0.85 | 7.5 | 380 | 94.3 | 67.3 | 528 | 3.8 |
| 4 | 236 | 0.51 | 20 | 0.85 | 0.85 | 7.5 | 382 | 94.2 | 67.8 | 542 | 3.87 |
| 5 | 236 | 0.49 | 20 | 0.85 | 0.85 | 7.5 | 382 | 94.1 | 68.2 | 555 | 3.94 |
La prova che la scelta dei poli deriva dal calcolo della densità superficiale di corrente alla temperatura limite di funzionamento, si è ottenuta annullando le perdite nel ferro e le perdite addizionali nei calcoli termici (vedere Paragrafo 1.8): l’ottimizzazione effettuata con questa approssimazione ha fornito una macchina finale che aveva 28 poli.
L’ultima ottimizzazione che si vuole effettuare con queste specifiche ha l’obiettivo di massimizzare contemporaneamente sia la coppia che il rendimento. E’ interessante, infatti, studiare il comportamento di una funzione di prestazione definita in questo modo:
I coefficienti a1 e a2 sono dei pesi assegnati a ciascuna grandezza per definirne l’importanza nell’ottimizzazione. Il metodo multiobiettivo permette di studiare le due grandezze che sono libere dai vincoli. A parte l’interesse pratico del problema questo tipo di implementazione consente di capire quale è il legame tra le due grandezze in gioco. In generale, infatti, si presenteranno due casi: una grandezza potrebbe massimizzarsi prevalendo sull’altra; oppure le due grandezze potrebbero crescere concordemente.
L’ottimizzazione verrà effettuata con l’obiettivo di raggiungere il 100 % del rendimento con coppia media pari a 250 [Nm]. Ai pesi delle due funzioni sono stati assegnati i seguenti valori: a1=0.4 [N-1m-1]; a2=1.
In questo caso dai risultati della Tabella 4-8 si osserva che la coppia ed il rendimento di macchina sono delle funzioni piuttosto concordi.
Tabella 4-8 Ottimizzazione multiobiettivo
| Rest | Kr | Poli | Kpest | Kpint | Azcu | F(P) | Tm | hm | Peso | Perdite | Jt | |
| Unità [mm] [mm] [Nm] [kg] [W] [A/mm2] | ||||||||||||
| Powell | ||||||||||||
| 1 | 200 | 0.75 | 24 | 0.7 | 0.7 | 3 | 128 | 94.5 | 90.5 | 21.5 | 229 | 5.01 |
| 10 | 200 | 0.75 | 24 | 0.85 | 0.85 | 7.5 | 160 | 163 | 94.3 | 33.6 | 229 | 3.11 |
| 20 | 200 | 0.5 | 24 | 0.85 | 0.85 | 7.5 | 183 | 225 | 93.3 | 41.6 | 374 | 3.78 |
| 30 | 200 | 0.49 | 21.4 | 0.85 | 0.85 | 7.5 | 184 | 226 | 93.2 | 44 | 379 | 3.84 |
| 40 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| 50 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| 60 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| 61 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| 62 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| Box | ||||||||||||
| 1 | 236 | 0.42 | 21.4 | 0.85 | 0.85 | 7.5 | 244 | 375 | 93.6 | 66.5 | 592 | 4.2 |
| 2 | 236 | 0.44 | 20 | 0.85 | 0.85 | 7.5 | 245 | 379 | 93.7 | 68.7 | 582 | 4.12 |
| 3 | 236 | 0.46 | 20 | 0.85 | 0.85 | 7.5 | 246 | 381 | 93.9 | 68.5 | 571 | 4.04 |
| 4 | 236 | 0.48 | 20 | 0.85 | 0.85 | 7.5 | 247 | 382 | 94 | 68.3 | 559 | 3.96 |
| 5 | 236 | 0.5 | 20 | 0.85 | 0.85 | 7.5 | 247 | 382 | 94.2 | 67.9 | 546 | 3.89 |
| 6 | 236 | 0.49 | 20 | 0.85 | 0.85 | 7.5 | 247 | 382 | 94.1 | 68.1 | 553 | 3.93 |
| 7 | 236 | 0.5 | 20 | 0.85 | 0.85 | 7.5 | 247 | 382 | 94.1 | 68 | 550 | 3.91 |
| 8 | 236 | 0.49 | 20 | 0.85 | 0.85 | 7.5 | 247 | 382 | 94.1 | 68.1 | 551 | 3.92 |
Se non ci sono vincoli restrittivi sulle funzioni di prestazione l’ottimizzazione multiobiettivo può risultare il metodo di studio più efficace. E’ necessario però, porre particolare attenzione nell’assegnazione dei pesi su ogni funzione obiettivo. Bisogna notare che questi coefficienti non riflettono proporzionalmente l’importanza relativa dei diversi obiettivi, ma sono solamente dei fattori che, quando sono variati, modificano la posizione del risultato dell’ottimizzazione. Nello spazio delle variabili di stato, la posizione della soluzione, infatti, dipende anche dalle unità di misura in cui le funzioni obiettivo sono espresse: se si desidera che i coefficienti ai riflettano strettamente l’impostazione degli obiettivi è necessario che tutte le funzioni siano espresse da valori numericamente simili.
Le ottimizzazioni effettuate elaborando diverse problematiche su coppia di macchina e rendimento hanno sempre condotto a dedurre i seguenti criteri di progettazione:
– L’ingombro radiale viene sempre occupato totalmente per diverse ragioni: la coppia e più elevata perché il braccio viene massimizzato; lo spazio disponibile per l’avvolgimento delle bobine viene maggiormente sfruttato; è maggiore la velocità periferica della macchina, cioè il coefficiente di convezione termica;
– Il numero di poli da scegliere e stato spesso il minore possibile. Le ragioni sono state esposte precedentemente.
– Lo spazio occupato dai magneti è stato sempre il massimo ammissibile dai vincoli strutturali imposti nel Paragrafo 4.1.
4.4 OTTIMIZZAZIONE DELLA COPPIA SPECIFICA
Nel Paragrafo 2.4 è stata già messa in evidenza l’importanza che la coppia specifica presenta per una macchina a flusso assiale. Il calcolo del peso della macchina sarà effettuato aggiungendo al peso delle parti attive il peso dei rotori. I dischi rotorici non vengono calcolati a flessione per i motivi spiegati nel Paragrafo 1.9. In pratica, il peso del rotore calcolato solo con il criterio elettrico potrebbe essere spesso minore di quello reale.
Nella Tabella 4-9 sono riportate alcune ottimizzazioni della coppia specifica eseguite su motori con raggi di ingombro (Ring) diversi, che hanno velocità di rotazione pari a 250 rpm. La temperatura di funzionamento vale 85 °C e sarà mantenuta costante durante l’ottimizzazione. I motori vengono alimentati con corrente di forma d’onda sinusoidale. A parte i vincoli strutturali che devono essere sempre presenti non viene assegnata nessun altra condizione dimensionale o di prestazione. Per ogni ottimizzazione si riporta solo la soluzione finale.
Visti i risultati ottenuti è possibile effettuare i seguenti rilievi:
– I rapporti tra i raggi della macchina sono variabili tra 0.71 e 0.56 con una tendenza a diminuire all’aumentare del raggio di ingombro. Se si tenesse conto anche del dimensionamento a flessione della macchina probabilmente questi parametri sarebbero più elevati perché il sistema troverebbe un equilibrio tra le forze di attrazione proporzionali anche alle dimensioni dei magneti e lo spessore dei rotori.
– Il numero di poli cresce fino al massimo ammissibile per la frequenza di alimentazione. La riduzione permette, infatti, di abbassare lo spessore dello statore e dei rotori diminuendo anche il peso del rame sulle testate.
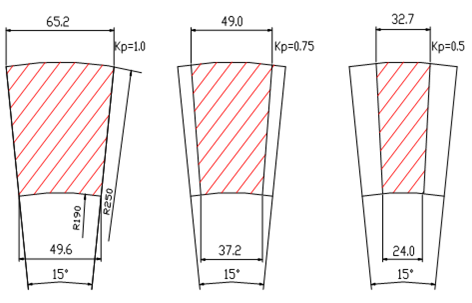
– La forma dei magneti si è ridotta rispetto ai risultati ottenuti nel paragrafo precedente. Si può anche notare come il rapporto Kp sul raggio interno è leggermente minore di quello sul raggio esterno. In pratica, avviene che il modello di ottimizzazione cercando di ridurre la superficie dei magneti riesce a farlo maggiormente sul raggio interno dove si produce la coppia minore.
Tabella 4-9 Ottimizzazioni della coppia specifica con diversi raggi di ingombro
| Ring | Rest | Kr | Poli | Kpest | Kpint | Azcu | F(P) | Tm | hm | Peso | Perdite | Jt |
| Unità [mm] [mm] [Nm/kg] [Nm] [kg] [W] [A/mm2] | ||||||||||||
| 80 | 72,7 | 0.71 | 28 | 0.6 | 0.58 | 3 | 2.1 | 2.87 | 76.4 | 1.35 | 23.2 | 4.25 |
| 100 | 89.8 | 0.64 | 28 | 0.58 | 0.57 | 3.2 | 2.8 | 7.72 | 80.4 | 2.71 | 49.2 | 4.54 |
| 120 | 110 | 0.63 | 28 | 0.57 | 0.55 | 3.3 | 3.5 | 15 | 83 | 4.33 | 80.6 | 4.76 |
| 140 | 130 | 0.61 | 28 | 0.55 | 0.54 | 3 | 4 | 25.1 | 84.2 | 6.27 | 124 | 5.18 |
| 160 | 146 | 0.6 | 28 | 0.59 | 0.57 | 6.7 | 4.8 | 60.3 | 90.6 | 12.5 | 163 | 3.56 |
| 180 | 166 | 0.59 | 28 | 0.57 | 0.57 | 7.1 | 5.4 | 92.7 | 91.6 | 17.1 | 223 | 3.58 |
| 200 | 186 | 0.59 | 28 | 0.56 | 0.56 | 7.2 | 6 | 135 | 92.4 | 22.4 | 291 | 3.62 |
| 220 | 206 | 0.58 | 28 | 0.55 | 0.54 | 7.2 | 6.6 | 186 | 92.9 | 28.3 | 372 | 3.7 |
| 240 | 226 | 0.58 | 28 | 0.55 | 0.54 | 7.3 | 7.1 | 251 | 93.4 | 35.3 | 465 | 3.76 |
| 260 | 246 | 0.58 | 28 | 0.56 | 0.52 | 7.3 | 7.6 | 330 | 93.8 | 43.3 | 568 | 3.81 |
| 280 | 266 | 0.57 | 28 | 0.53 | 0.52 | 7.4 | 8.1 | 421 | 94.1 | 51.9 | 690 | 3.87 |
| 300 | 286 | 0.56 | 28 | 0.54 | 0.51 | 7.3 | 8.6 | 529 | 94.4 | 61.6 | 822 | 3.94 |
| 320 | 306 | 0.56 | 28 | 0.53 | 0.5 | 7.4 | 9.1 | 654 | 94.7 | 72.2 | 965 | 3.98 |
– In tutte le soluzioni lo spessore Azcu della bobina non raggiunge mai il limite imposto di 7.5 mm. Addirittura per raggi di ingombro inferiori a 140 mm Azcu rimane sempre intorno ai 3 mm. Questa tendenza può spiegarsi considerando che per raggi di ingombro ridotti il peso del rame assume una quota parte rilevante nel peso totale delle parti calcolate.
– Osservando il calcolo delle altre grandezze di prestazione si nota una piccola riduzione della densità superficiale di corrente all’aumentare del raggio di ingombro. Le bobine delle macchine più piccole vengono perciò sfruttate maggiormente. Anche per questo motivo si evidenzia un innalzamento del rendimento della macchina.
Nella Tabella 4-10 sono riportati i risultati di 13 ottimizzazioni effettuato fissando come funzione obiettivo il rapporto tra la coppia media della macchina ed il solo peso dei due dischi rotorici.
Questo studio è interessante perché si distingue il peso delle parti rotoriche che partecipano alla rotazione del complesso motore carico ed il peso delle parti statoriche che sono invece fissate con il telaio. Durante il funzionamento di un motore la ripartizione del peso tra le due parti può risultare di rilevante importanza. La differenza più evidente rispetto alle soluzioni della Tabella 4-9 è la diminuzione del passo polare occupato dai magneti, con un conseguente aumento dello spessore della bobina. Il modello di ottimizzazione ha seguito il criterio di produrre la potenza meccanica abbassando i valori efficaci delle fem indotte nelle bobine di macchina aumentando viceversa la corrente di alimentazione. Questa scelta comporta una riduzione sostanziale della coppia e del rendimento. La riduzione del peso delle parti rotoriche comporta comunque la possibilità di ridurre anche lo spessore dello statore: i pesi delle macchine calcolate sono molto minori di quelli della Tabella 4-10.
Tabella 4-10 Ottimizzazioni del rapporto coppia-peso dischi rotorici per diversi raggi di ingombro
| Ring | Rest | Kr | Poli | Kpest | Kpint | Azcu | F(P) | Tm | hm | Peso | Perdite | Jt | ||
| Unità [mm] [mm] [Nm/kg] [Nm] [kg] [W] [A/mm2] | ||||||||||||||
| 80 | 70 | 0.71 | 28 | 0.46 | 0.43 | 3 | 3.6 | 2.23 | 71.6 | 1.09 | 23.2 | 4.34 | ||
| 100 | 85.5 | 0.7 | 28 | 0.36 | 0.34 | 7.5 | 5.7 | 6.11 | 80.8 | 2.55 | 38.1 | 2.97 | ||
| 120 | 106 | 0.69 | 28 | 0.35 | 0.3 | 7.5 | 7.1 | 12.1 | 83 | 4.06 | 64.9 | 3.13 | ||
| 140 | ||||||||||||||
| 89.1 | 22.7 | 442 | 3.75 | |||||||||
| 260 | 246 | 0.54 | 28 | 0.26 | 0.32 | 7.5 | 15.2 | 191 | 89.3 | 29.1 | 598 | 3.98 |
| 280 | 266 | 0.54 | 28 | 0.25 | 0.23 | 7.5 | 16.2 | 212 | 88.5 | 32 | 719 | 4.05 |
| 300 | 286 | 0.55 | 28 | 0.24 | 0.23 | 7.5 | 17.3 | 259 | 89.1 | 37.1 | 832 | 4.06 |
| 320 | 306 | 0.58 | 28 | 0.23 | 0.23 | 7.5 | 18.3 | 313 | 89.8 | 42.3 | 930 | 4.03 |