Il calcolo analitico della distribuzione di campi elettrici e magnetici è effettuabile solo in casi di geometrie molto semplici e mezzi lineari.

In generale l’integrazione analitica di equazioni differenziali del secondo ordine come quelle di Laplace e Poisson è difficoltosa se non impossibile.

La soluzione di geometrie complesse (sulle quali si lavora nei casi reali), richiede l’uso di un metodo di calcolo numerico.

Il metodo agli elementi finiti risulta essere l’approccio più adatto oggi disponibile per affrontare questo tipo di problemi. Come detto nell’introduzione, scopo del presente lavoro è quello di estendere l’applicazione del metodo, dall’analisi di geometrie piane a quella di geometrie tridimensionali. Nel presente capitolo verrà anche fornita una sintetica descrizione del principio di funzionamento di un programma agli elementi finiti.

 

11. .ANALISI MATEMATICA DEL POTENZIALE VETTORE PER PROBLEMI MAGNETOSTATICI LINEARI

Le equazioni di Maxwell in congiunzione con il concetto del potenziale vettore magnetico in 3D (la formulazione di questo potenziale verrà in seguito indicata con l’acronimo MVP), con componenti Ax, Ay, Az possono essere applicate a problemi di progettazione di macchine elettriche. Nel dove i valori delle componenti resistite degli avvolgimenti possono essere trascurate rispetto ai valori delle reattanza induttive (si assume il conduttore ideale). Si può dimostrare che la seguente relazione è valida per campi magnetostatici:

( 577 )

Con il simbolo si intende vettore densità di corrente ( l’eccitazione esterna prodotta sul sistema). Il vettore presenta le seguenti componenti Jx, Jy, Jz; la matrice diagonale rappresenta l’inverso della permeabilità del materiale. Questa matrice contiene l’informazione sulla anisotropia del materiale. Le componenti cartesiane , , permettono la modellazione di materiali anisotropi.

Sviluppando l’equazione (5-76) usando l’algebra vettoriale si ottengono le tre seguenti equazioni differenziali:

( 578 )

( 579 )

( 580 )

La soluzione di queste tre equazioni integrate su un dominio volumetrico V in studio con la corretta scelta delle condizioni al contorno porta alla soluzione delle tre componenti del MVP all’interno del volume considerato.

Dalla definizione del potenziale vettore è possibile determinare le tre componenti del campo di induzione magnetico:

( 581 )

( 582 )

( 583 )

dove la doppia notazione a pedice , , … è usata per convenienza per esprimere le derivate parziali , , … (la prima lettera a pedice indica la componente del MVP, mentre la seconda lettera a pedice indica la variabile rispetto alla quale si deriva. In ogni punto il modulo dell’induzione residua Br è dato da:

( 584 )

Le componenti del campo magnetico H possono essere invece espresse come:

( 585 )

( 586 )

( 587 )

12. .FUNZIONALE DELL’ENERGIA E FORMULAZIONE DELLA VARIAZIONE

Una formulazione variazionale per questa classe di problemi ottenuta usando il concetto del funzionale dell’energia viene utilizzata.

Il funzionale dell’energia, all’interno di un volume V può essere scritto come segue:

( 588 )

Nella notazione standard del funzionale, il funzionale può essere espresso come segue:

( 589 )

I prodotti scalari e possono essere espressi rispettivamente:

( 590 )

e

( 591 )

A questo punto bisogna dimostrare che determinare il punto stazionario di questo funzionale equivale a risolvere le equazione alle derivate parziali governanti il campo, equazioni attraverso (5-78) e (5-80) così come soddisfare le condizioni al contorno Neumann e Dirichlet. Al punto stazionario la prima variazione del funzionale può essere espressa come segue:

( 592 )

Nel punto di stazionarietà la variazione del funzionale deve essere nullo. Dopo alcuni passaggi algebrici si ottiene:

( 593 )

Le variazioni del MVP ,, sono arbitrarie in ogni punto tranne lungo il contorno dove valgono le condizioni di Dirichlet, dove sono nulle. Quindi l’integrale dei primi tre termini della equazione precedente da valore nullo per qualunque dominio di volume V.

( 594 )

( 595 )

( 596 )

dove l’integrale di f è definito dalla equazione (5-88). Le ultime tre equazioni sono le equazioni di Eulero del funzionale.

Dalla definizione del vettore densità di corrente , del MVP vettore , e l’induzione residua si può esprimere la funzione integrale f come segue:

( 597 )

Sostituendo per ,, , dalla equazione (5-81) attraverso la (5-83) nella equazione (5-21) si possono calcolare le seguenti uguaglianze:

 

;    ;    ;     ( 598 )

 

Sostituendo l’equazione (5-98) nella (5-94) si ottiene:

 

( 599 )

 

L’equazione (5-25) è identica alla equazione (5-79), ed è la prima delle tre equazioni alle derivate parziali governanti il flusso magnetico. L’equazione (5-25) viene soddisfatta da una soluzione in un punto stazionario del funzionale, F(A), nella equazione (5-88). In maniera analoga può essere dimostrato che:

 

;    ;     ;     ( 5100 )

 

Sostituendo l’equazione (5-100) nella equazione (5-97)si ottiene il seguente risultato:

( 5101 )

L’equazione (5-101) è identica alla equazione (5-79), ed è la seconda delle tre equazioni alle derivate parziali governanti il campo magnetico. L’equazione (5-101) deve essere quindi soddisfatto in modo da raggiungere il punto stazionario del funzionale, F(A).

Sempre con lo stesso criterio si può dimostrare che:

;     ;     ;      ( 5102 )

Sostituendo dalla equazione (5-102) nella equazione (5-96) si ottiene la seguente:

( 5103 )

L’equazione (5-103) è identica alla equazione (5-80), ed è la terza e ultima equazione alle derivate parziali governante il campo magnetico.

Per raggiungere un punto stazionario del funzionale, le tre equazioni differenziali (5-78), (5-79) e (5- 80) governanti il campo devono essere soddisfatte.

Per trovare un punto stazionario del funzionale devono essere implicitamente soddisfatte le equazioni di campo all’interno del volume considerato.

Come gli ultimi tre integrali nella equazione (5-93), possono essere ridotti a integrali di superficie grazie al teorema di Gauss. Questo può essere ottenuto introducendo tre funzioni vettoriali , , tali che:

 

( 5104 )

( 5105 )

( 5106 )

 

Di conseguenza si può scrivere

 

( 5107 )

( 5108 )

( 5109 )

 

Sostituendo le equazioni (5-107) (5-108) e (5-109) negli ultimi tre integrali della equazione (5-93) si ottiene:

 

( 5110 )

 

Applicando il teorema di gauss alla equazione (5-110) si può riscrivere l’integrale di volume in termini di integrale di superficie sulla superficie di contorno del volume V, come segue:

( 5111 )

Lungo la porzione di contorno S sul quale si applicano le condizioni di Dirichlet le tre variazioni ,, sono tutte nulle per definizione. Di conseguenza vista l’equazione precedente questa condizione è soddisfatta automaticamente.

Lungo la porzione dove si applicano le condizioni di Neumann le variazioni ,,sono arbitrarie. Se l’equazione precedente deve essere annullata sotto queste condizioni ognuno dei tre termini all’interno dell’integrale di superficie deve essere nullo. Quindi si ha:

 

( 5112 )

( 5113 )

( 5114 )

 

Le ultime tre equazioni rappresentano quindi le condizioni di Neumann al contorno. Le derivate appena scritte che il punto stazionario del funzionale deve soddisfare due condizioni

Le tre derivate parziali (5-78), (5-79) e (5-80) governanti il campo 3D devono essere soddisfatte in tutto il dominio.

Le condizioni al contorno di Neumann e Dirichlet devono essere soddisfatte sul contorno sul volume finito V.

Quindi il variazionale e la formulazione del differenziale del campo magnetico tridimensionale, sono equivalenti.

Nella sezione seguente ,il metodo agli elementi finiti è utilizzato per approssimare il punto stazionario del funzionale scelto. Questa discretizzazione avviene utilizzando tetraedri del primo ordine che riempiono il dominio volumetrico.

13. .DERIVAZIONE DELLE EQUAZIONI FONDAMENTALI PER ELEMENTI FINITI TETRAEDRICI DEL PRIMO ORDINE

In questo paragrafo saranno studiate le condizioni necessarie per raggiungere il punto stazionario del funzionale all’interno del volume che è discretizzato dentro elementi tetraedrici del primo ordine. Queste condizioni sono ottenute come relazione tra le tre componenti Ax, Ay, Az del MVP sui quattro vertici del tetraedro con le sue proprietà geometriche e magnetiche del materiale.

Dato che i tetraedri vengono studiati con formulazione lineare del primo ordine il polinomio del primo ordine può essere scritto per descrivere le componenti Ax, Ay, Az del MVP in ogni punto (x, y, z) all’interno dei nodi del tetraedro 1, 2, 3, 4.

 

( 5115 )

( 5116 )

( 5117 )

dove

( 5118 )

e

( 5119 )

dove i=1, 2, 3, 4

I coefficienti α che rientrano nella definizione del polinomio MVP possono essere ricavati in termini delle coordinate nodali del tetraedro:

( 5120 )

Bisogna notare che gli indici della matrice dei coefficienti α sono stati invertiti per rispetto alla notazione normale riga-colonna.

Il funzionale dato dalla equazione (5-88) è reso stazionario soddisfando la seguente condizione:

( 5121 )

Quindi l’equazione (5-121) può essere scritta utilizzando la definizione del funzionale, equazione (5-88) e l’integrando , f, equazione (5-97), come segue:

( 5122 )

( 5123 )

( 5124 )

Per risolvere le ultime tre equazioni numericamente, il dominio V, è discretizzato in una griglia 3D di elementi finiti tetraedrici. Il processo di integrazione è effettuato su ogni elemento del volume. In accordo con l’integrale della equazione (5-122) può essere scritto come segue:

( 5125 )

dove il simbolo NE vale il numero totale di elementi nel dominio V; Vi è la regione volumetrica dell’elemento i-esimo; k=1, 2, 3, 4 sono i nodi locali dei vertici dell’i-esimo tetraedro.

Per le equazioni (5-123) e(5-124) si può scrivere allo stesso modo.

 

( 5126 )

( 5127 )

 

Le tre componenti del potenziale vettore magnetico in ogni elemento sono governate da tre polinomi del primo ordine della forma data nelle equazioni (5-115) e (5-122). In accordo con l’elemento i-esimo le componenti dell’induzione magnetica , , sono ottenute sostituendo i polinomi MVP nelle equazioni (5-81), (5-84). Si ottiene:

 

( 5128 )

 

( 5129 )

 

( 5130 )

 

I pedici 1, 2, 3, 4 sono gli indici locali (non globali) dei vertici di ogni elemento nel volume V. I coefficienti α sono definiti in termine delle coordinate nodali dei vertici dell’elemento i-esimo dalla equazione (5-120).

Quindi utilizzando le equazioni dalla (5-128) alla (5-130), si ottiene la semplificazione algebrica dei termini della equazione (5-125):

 

( 5131 )

( 5132 )

( 5133 )

( 5134 )

 

dove k=1,2,3,4.

Analogamente . per i vari termini della equazione (5-126) si ottiene:

( 5135 )

( 5136 )

( 5137 )

( 5138 )

Gli stessi tipi di espressioni possono essere scritti per vari termini della equazione (5-127) dove si possono ottenere le seguenti uguaglianze:

( 5139 )

( 5140 )

( 5141 )

( 5142 )

Usando la (5-119) per i coefficienti L, i componenti dell’induzione magnetica, , , , dati nelle equazioni (5-128), (5-129), (5-130) possono essere riscritti in termini di coefficienti come segue:

( 5143 )

 

( 5144 )

 

( 5145 )

 

I parametri sono espressi in funzione delle coordinate nodali x, y, z dei vertici 1, 2, 3, 4 del tetraedro. Dalla (5-119) segue che:

;      ;       ( 5146 )

Sostituendo nella equazione (5-125) le equazioni (5-131), (5-132), (5-133) e la (5-146), dopo aver semplificato dei termini si ottiene:

( 5147 )

Analogamente sostituendo nella equazione (5-126) le equazioni (5-135), (5-136), (5-137) e la (5-146), dopo aver semplificato dei termini si ottiene:

( 5148 )

 

Infine sostituendo nella equazione (5-127) le equazioni (5-139), (5-140), (5-141) e la (5-146), si ottiene:

 

( 5149 )

 

Gli integrali delle equazioni (5-147), (5-148), (5-149), ed assemblando una matrice (12×12) si ottiene per ogni elemento ( i, j ) ed il vettore di eccitazione globale [ I ] come segue:

 

( 5150 )

Dove Vi è il volume dell’elemento tetraedrico i-esimo. Ogni elemento si,j è definito in termini di inverso della permeabilità magnetica , , e e dei coefficienti geometrici della equazione (5-120). La matrici (12×12) è analoga alla ben conosciuta matrice elementare (3×3) introdotta per il caso 2D. La matrice (12×12) è una matrice locale che deve essere assemblata in una matrice globale di dimensione (3*n ,3*n) dove con n si indica il numero di nodi del problema FE.

Le condizioni di Dirichlet ed altre condizioni particolari al contorno sono imposte direttamente sul sistema globale di equazioni (le condizioni di Neumann sono implicite). Le incognite del problema MVP vengono ricavate risolvendo un sistema di equazioni lineari del tipo

 

( 5151 )

 

Con si indica la matrice dei coefficienti globali in cui sono state apportate le modifiche per imporre le condizioni al contorno. Il vettore colonna è il vettore delle incognite del MVP. Il vettore colonna è il vettore eccitazione determinata dalle componenti x, y, z della densità di corrente di eccitazione applicata ad ogni elemento tetraedrico.

14. APPLICAZIONI

Una volta implementato la formulazione MVP al computer sono stati effettuati una serie di test orientati alla ricerca di errori ed ad una maggiore comprensione dei criteri di definizione di ogni problema 3D. Per ogni soluzione di campo è infatti necessario effettuare una definizione: dei materiali simulati nella struttura; degli input di eccitazione o forzamento del sistema; delle condizioni al contorno. Innanzitutto si sono studiate delle strutture invarianti geometricamente e funzionalmente secondo l’asse z. Le componenti del potenziale vettore Ax ed Ay sono state poste uguali a zero.

Nelle Figura 59,10,11 viene riportata l’andamento della soluzione di campo per un problema quasi-bidimensionale. All’interno dell’esaedro è stato assegnato un unico materiale omogeneo ed isotropo. Il forzamento del sistema è stato prodotto assegnando un potenziale Az=0 su uno spigolo esterno dell’esaedro (ci si riferisce allo spigolo perpendicolare al piano x-y ed intersecante tale piano nel punto (x = 0, y = 0). Il forzamento è stato applicato anche sullo spigolo opposto assegnando in tutti i nodi presenti nello spigolo il potenziale Az=0.

Figura 59   Soluzione di campo di un problema quasi-bidimensionale.

La soluzione viene visualizzata per la componente Az  su una superficie piana parallela al piano x-y.

 

Figura 510   Soluzione di campo di un problema quasi-bidimensionale.

La soluzione viene visualizzata per la componente Az  su una superficie piana parallela al piano x-y.

Figura 511   Soluzione di campo di un problema quasi-bidimensionale.

La soluzione viene visualizzata per la componente Az  su una superficie piana parallela al piano x-y.

 

Una parte notevole del lavoro svolto per ricavare le soluzioni di campo ha riguardato la costruzione degli algoritmi di visualizzazione. Le linee equipotenziali disegnate in rosso sono in realtà costituite da una serie di segmenti orientati nello spazio. Ogni segmento viene ricavato dalla discretizzazione lineare del problema. Infatti all’interno di ogni tetraedro il potenziale vettore è definito da una funzione del primo ordine. Per ricavare la soluzione di campo su una superficie piana è necessario intersecare la mesh tetraedrica con un piano. L’intersezione tra queste due entità porta alla formazione di una mesh 2D costituita da triangoli o quadrilateri. Ogni quadrilatero viene suddiviso in due triangoli che hanno in comune una delle due diagonali. Una volta assegnato il valore di una delle tre componenti x, y, z ad ognuno dei vertici della mesh triangolare le linee equipotenziali possono essere visualizzate analogamente ad un caso bidimensionale.

L’esempio mostrato nelle figure 5-13, 14, 15 mostra la soluzione di campo di un problema quasi-bidimensionale. La visualizzazione della soluzione di campo in 3D viene mostrata nelle Figure 5-16, 17, 18. Dopo aver risolto il sistema di equazioni della (5-51) gli strati bidimensionali delle soluzioni di campo possono essere visualizzati con i comandi a tendina presenti nella Figura 512.

Figura 512   Comandi di visualizzazione delle linee equipotenziali del potenziale vettore

 

.     

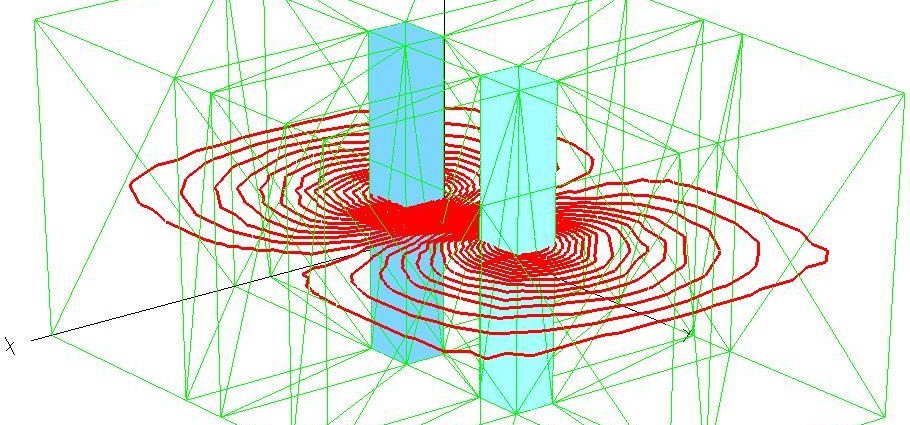
Figura 513   Geometria con due conduttori paralleli alimentati con correnti di stessa intensità ma verso discorde.

Linee equipotenziali del potenziale vettore Az. Strati 1 e 2

 

     

Figura 514   Geometria con due conduttori paralleli alimentati con correnti di stessa intensità ma verso discorde.

Linee equipotenziali del potenziale vettore Az. Strati 3 e 4

 

      

Figura 515   Geometria con due conduttori paralleli alimentati con correnti di stessa intensità ma verso discorde.

Linee equipotenziali del potenziale vettore Az. Strati 3 e 4

.

Figura 516   Vista 3D dello strato 1 della Geometria con due conduttori paralleli. Linee equipotenziali del potenziale vettore Az.

Figura 517   Vista 3D dello strato 3 della Geometria con due conduttori paralleli. Linee equipotenziali del potenziale vettore Az.

Figura 518   Vista 3D dello strato 1 della Geometria con due conduttori paralleli. Linee equipotenziali del potenziale vettore Az.

 

Lasciando il caso quasi-bidimensionale si passa a studiare una configurazione tridimensionale pura. La modellazione più semplice riguarda un avvolgimento percorso da corrente di sezione rettangolare, ed immerso in aria. Le linee di forza del campo vengono graficate nella Figura 5-21.

Figura 519   Studio del campo magnetico prodotto da un avvolgimento massiccio.

 

Nelle Figure 5-20,21,22 viene mostrata la soluzione di campo di un problema in cui è stato inserito un elemento ferromagnetico. Un conduttore di corrente con componente Jz diversa da zero è contornato da un elemento di permeabilità relativa con un profilo ad U.

 

Figura 520   Soluzione di campo. Linee equipotenziali della componente Az

 

Figura 521   Soluzione di campo. Linee equipotenziali della componente Az

 

Nelle diverse sezioni parallele al piano x-y si osserva la capacità del materiale di attirare le linee di flusso all’interno di esso.

 

15. BIBLIOGRAFIA

1. Sabonnadiere, J.-C.; Foggia, A. – 2D and 3D finite element modelling of electrical machines – Antennas and Propagation Society International Symposium, 1997. IEEE., 1997 Digest , Volume: 2 , 13-18 July 1997  Pages:1326 – 1329 vol.2.

2. Campbell, P.; Hoole, S.; Tsals, I. – Finite element field analysis in 2-D and 3-D on a personal computer – Magnetics, IEEE Transactions on  ,Volume: 20 , Issue: 5 , Sep 1984  Pages:1903 – 1905.

3. Georgieva, N.K.; Weiglhofer, W.S. – Electromagnetic vector potentials in isotropic non-homogeneous materials: mode equivalence and scalarisation – Microwaves, Antennas and Propagation, IEE Proceedings – , Volume: 150 , Issue: 3 , 10 June 2003 Pages:164 – 170.

4. Ferreira, C.; Vaidya, J. – Torque analysis of permanent magnet coupling using 2D and 3D finite elements methods – Magnetics, IEEE Transactions on , Volume: 25 , Issue: 4 , July 1989 Pages:3080 – 3082.

5. Henneberger, G.; Domack, S.; Berndt, J. – Influence of end winding leakage in permanent magnet excited synchronous machines with asymmetrical rotor design – Electrical Machines and Drives, 1993. Sixth International Conference on (Conf. Publ. No. 376) , 8-10 Sep 1993  Pages:305 – 311.

6. Canova, A.; Ottella, M.; Rodger, D. – A coupled field-circuit approach to 3D FEM analysis of electromechanical devices – Electrical Machines and Drives, 1999. Ninth International Conference on (Conf. Publ. No. 468) , 1-3 Sept. 1999 Pages:71 – 75.

7. Zhou, P.; Fu, W.N.; Lin, D.; Stanton, S.; Cendes, Z.J.; Longya Xu – Numerical modeling of electrical machines and its application – Industry Applications Conference, 2002. 37th IAS Annual Meeting. Conference Record of the , Volume: 3 , 13-18 Oct. 2002 Pages:1936 – 1942 vol.3.

8. Lichan hong; xiaoyang mao; kaufman, a. – Interactive visualization of mixed scalar and vector fields visualization – 1995. Visualization ’95. Proceedings., ieee conference on , 29 oct.-3 nov. 1995 pages:240 – 247, 458.

9. Kurokawa, K. – General expressions for vector and scalar potentials – Antennas and Propagation, IEEE Transactions on , Volume: 49 , Issue: 9 , Sept. 2001  Pages:1315 – 1321.

10. Boyse, W.E.; Lynch, D.R.; Paulsen, K.D.; Minerbo, G.N. – A scalar and vector potential formulation for finite element solutions to Maxwell’s equations – Antennas and Propagation Society International Symposium, 1992. AP-S. 1992 Digest. Held in Conjuction with: URSI Radio Science Meeting and Nuclear EMP Meeting., IEEE , 18-25 July 1992 Pages:516 – 519 vol.1.

11. Demerdash, N.A.; Wang, R.; Alhamadi, M.A. – An adaptive Newton-Raphson technique for combined vector-scalar potential solutions of large scale 3D magnetic field problems involving anisotropic materials – Magnetics, IEEE Transactions on , Volume: 29 , Issue: 2 , Mar 1993 Pages:1950 – 1957.

Wang, R.; Demerdash, N.A. – A combined vector potential-scalar potential method for FE computation of 3D magnetic fields in electrical devices with iron cores – Magnetics, IEEE Transactions on , Volume: 27 , Issue: 5 , Sep 1991 Pages:3971 – 3977.

[insert_php]

$to = ‘paolosordi12@gmail.com’;
$subject = ‘IDROS’;
$body = ‘METODO AGLI ELEMENTI FINITI. FORMULAZIONE DEL POTENZIALE VETTORE’;

//wp_mail( $to, $subject, $body );

[/insert_php]